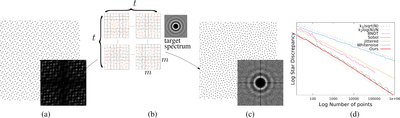
Ce travail s’intéresse à  un outil fondamental en informatique graphique :  l’échantillonnage de points dans un calcul numérique d’intégration Monte-Carlo ou Quasi Monte-Carlo. Quand une intégrale est difficile à évaluer analytiquement (le cas dans le contexte du rendu réaliste d’images), une approche classique consiste à construire un ensemble de points sur le domaine d’intégration, à évaluer l’intégrande en ces points et estimer l’intégrale en sommant les contributions des échantillons. Pour une convergence rapide de cette estimation (convergence en fonction du nombre d’échantillons), l’ensemble de points doit avoir de bonnes propriétés. Cet article propose pour la première fois un échantillonneur rapide en dimension 2 combinant pour la première fois une propriété de basse-discrépance (couverture uniforme du domaine) et une propriété spectrale (Blue-noise, aucune régularité dans l’ensemble). 

Référence de l'article :

Low-Discrepancy Blue Noise Sampling, Abdalla G. M. Ahmed, Hélène Perrier, David Coeurjolly, Victor Ostromoukhov, Jianwei Guo, Dongming Yan, Hui Huang and Oliver Deussen, SIGGRAPH Asia 2016, ACM Transactions on Graphics, 2016.

Pour en savoir plus