Formalisation et complexité combinatoire - symétries
Table of Contents
1 Compter sur les symétries
La résolution d'un problème de recherche peut parfois prendre une forme combinatoire (i.e., celle d'une stratégie pour la recherche d'un nœud solution dans un graphe d'états) car sa formalisation n'a pas pris en compte des contraintes propres au problème. Ces contraintes, facilement ignorées, prennent souvent la forme de symétries. On évitera ce piège en étant aussi parcimonieux que possible dans le choix du nombre de variables utilisées pour modéliser le problème de recherche.
2 Exemple du loup, de la chèvre et du chou
2.1 Enoncé
Un batelier doit faire passer un loup, une chèvre et un chou de l'autre côté de la rivière. Il n'a qu'une place sur son bateau. Si la chèvre et le chou sont laissés sans surveillance sur une rive, la chèvre mange le chou. Si la chèvre et le loup sont laissés sans surveillance sur une rive, le loup mange la chèvre.
2.2 Formalisation
La situation initiale formulée naïvement est la suivante :
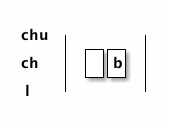
Les règles du jeu formulées naïvement sont les suivantes :
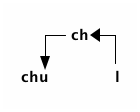
Mais en fait les deux relations qui forment les règles du jeu ne sont pas orientées. On voit alors que chou et loup sont fonctionnelement identiques (i.e., ils ne peuvent pas être sans surveillance en présence de la chèvre). Il n'est donc pas nécessaire ni souhaitable de leur donner des noms différents :
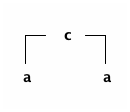
2.3 Résolution
Dans sa nouvelle formulation (et en s'interdisant de repasser par un état déjà rencontré), le problème n'est plus combinatoire : à chaque étape en direction du but, un seul choix est possible :
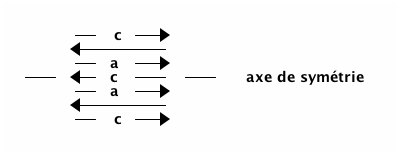
On peut remarquer en particulier l'axe de symétrie et le nombre impair de coups.
3 Exemple des époux jaloux
3.1 Enoncé
Trois couples doivent traverser une rivière grâce à un bateau à deux places. Chaque époux est jaloux : il ne veut pas qu'en son absence un autre homme soit en présence de son épouse.
3.2 Formalisation
On note \(C\) un couple, \(H\) un homme en l'absence de son épouse, \(F\) une femme en l'absence de son époux. On peut penser à d'autres notations (e.g., H1, F1, H2, F2, H3, F3). Mais nous sommes guidés par un critère de parcimonie dans le choix du nombre de variables afin de réduire le plus possible la complexité combinatoire du problème.
Il s'agit de trouver un programme \(S0\) qui fasse passer le système étudié de l'état \(\{3C||\}\) à l'état \(\{||3C\}\). Ce que l'on notera :
\begin{equation*} \{3C||\} \; S0 \; \{||3C\} \end{equation*}3.3 Résolution
Il semble facile de faire passer toutes les épouses de l'autre côté de la rivière. En profitant des symétries du problème, on rafine la spécification de \(S0\) :
\begin{equation*} \{3C||\} \\ S1 \\ \{3H||3F\} \\ S2 \\ \{3F||3H\} \\ S3 \\ \{||3C\} \end{equation*}On propose un programme qui répond à la spécification \(S1\) :
\begin{equation*} \{3C||\} \\ 1C2H|2F| \\ \{1C2H||2F\} \\ 1C2H|1F|1F \\ \{2C1H||1F\} \\ 3H|2F|1F \\ \{3H||3F\} \end{equation*}En profitant de la symétrie du problème, le programme \(S3\) se dérive automatiquement de \(S1\) :
\begin{equation*} \{3F||3H\} \\ 1F|2F|3H \\ \{1F||2C1H\} \\ 1F|1F|1C2H \\ \{2F||1C2H\} \\ |2F|1C2H \\ \{||3C\} \end{equation*}De plus, on sait que le programme \(S2\) contient l'axe de symétrie, il doit donc avoir pour forme :
\begin{equation*} \{3H||3F\} \\ S4 \\ 1C|1C|1C \\ S5 \\ \{3F||3H\} \end{equation*}Il y a nécessairement un nombre impair de coups et le premier coup était un déplacement de la rive gauche vers la rive droite. Dans quel sens sera le coup qui a lieu sur l'axe de symétrie ? Mettons, qu'il s'agisse d'un déplacement de la rive droite vers la rive gauche. Ainsi, l'état atteint après \(S4\) est \(\{1C||2C\}\). De même, l'état en précondition de \(S5\) est \(\{2C||1C\}\).
On propose un programme qui répond à la spécification \(S4\) :
\begin{equation*} \{3H||3F\} \\ 3H|1F|2F \\ \{1C2H||2F\} \\ 1C|2H|2F \\ \{1C||2C\} \end{equation*}Le programme S5 est obtenu automatiquement à partir de \(S5\) :
\begin{equation*} \{2C||1C\} \\ 2F|2H|1C \\ \{2F||1C2H\} \\ 2F|1F|3H \\ \{3F||3H\} \end{equation*}Nous venons de trouver la solution optimale en 11 coups sans recherche combinatoire (ou presque…).