Heuristiques pour la recherche dans un espace d'états
Table of Contents
- 1. Tous les noeuds atteignables à partir d'un noeud source
- 2. Recherche en largeur (breadth-first search)
- 3. Recherche en profondeur (depth-first search)
- 4. Plus court chemin sur un graphe aux arêtes étiquetées positivement (Dijkstra)
- 5. Plus court chemin en présence d'information contextuelle
- 6. Exemple sur le jeu de taquin de taille 8
- 7. Exemple sur le jeu de taquin de taille 15
- 8. Approfondissement itéré (iterative deepening)
- 9. Approfondissement itéré pour l'algorithme A* (IDA*)
1 Tous les noeuds atteignables à partir d'un noeud source
1.1 Dérivation du programme à partir de sa spécification
1.1.1 Première esquisse
Étant donné un graphe orienté G et un nœud \(v\) de ce graphe, nous cherchons à calculer l'ensemble des nœuds atteignables à partir de \(v\).
Nous notons \(s\) la fonction "successeur" qui retourne les voisins directs d'un ensemble de nœuds.
Nous définissons la fonction \(a\) ("atteignable") :
\begin{equation*} a(x) = x \cup a(s(x)) \end{equation*}Les solutions de cette équation sont de la forme \(a(u) = u\) (i.e., quand \(s(u) \subset u\) ).
L'ensemble des nœuds atteignables à partir de l'ensemble de nœuds \(x\) est le plus petit ensemble qui inclut \(x\) et qui est solution de l'équation ci-dessus. Sans cette précision, l'égalité ci-dessus ne pourrait pas servir de définition pour \(a\). Par exemple, quelque soit \(x\), l'ensemble de tous les nœuds du graphe satisferait cette égalité.
Notons qu'un tel plus petit ensemble solution existe. En effet, soient \(u\) et \(v\) deux solutions (i.e., \(a(u)=u\) et \(a(v)=v\) ). Il suffit de montrer que \(a(u) \cap a(v)\) est également solution. Il s'en suit qu'étant donné \(x\), il existe un plus petit ensemble solution incluant \(x\) (viz. l'intersection de tous les ensembles solution incluant \(x\) ).
Il s'agit de calculer un programme dont la post-condition est :
\begin{equation*} R: \;\; a(\{v\}) = x \end{equation*}Pour fixer les idées, nous pouvons avoir à l'esprit un exemple de graphe orienté (mais attention à ne pas être trop influencé par une configuration particulière…).
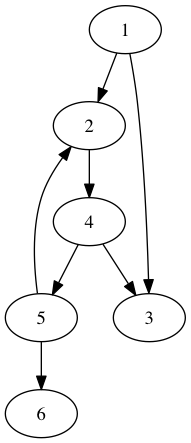
Figure 1: Graphe pour illustrer l'algorithme Atteignable
Nous avons par exemple :
\begin{equation*} a(\{4\}) = \{2,3,4,5,6\} \end{equation*}Nous cherchons une manière d'affaiblir la postcondition dans l'idée de découvrir un invariant. Nous remarquons :
\begin{equation*} a(x) = a(x \cup s(x)) \end{equation*}Pour le prouver, nous commençons par montrer :
\begin{equation*} \begin{aligned} & a(x \cup y) = a(x) \cup a(y) \\ \equiv \quad &\{\text{déf. de } a\} \\ & x \cup y \cup a(s(x \cup y)) = x \cup a(s(x)) \cup y \cup a(s(y)) \\ \equiv \quad &\{\text{algèbre}\} \\ & a(s(x \cup y)) = a(s(x)) \cup a(s(y)) \\ \equiv \quad &\{s(x \cup y) = s(x) \cup s(y)\} \\ & a(s(x) \cup s(y)) = a(s(x)) \cup a(s(y)) \\ \equiv \quad &\{\text{réc.}\} \\ & true \end{aligned} \end{equation*}Puis :
\begin{equation*} \begin{aligned} & a(s(x)) \subseteq a(x) \\ \Leftarrow \quad &\{\text{algèbre}\} \\ & a(x) = x \cup a(s(x)) \\ \equiv \quad &\{\text{déf. de } a\} \\ & true \end{aligned} \end{equation*}D'où :
\begin{equation*} \begin{aligned} & a(x \cup s(x)) \\ \equiv \quad &\{a(x \cup y) = a(x) \cup a(y)\} \\ & a(x) \cup a(s(x)) \\ \equiv \quad &\{a(s(x)) \subseteq a(x)\} \\ & a(x) \end{aligned} \end{equation*}Nous avons donc l'idée d'invariant :
\begin{equation*} P0 : \quad a(\{v\}) = a(x) \end{equation*}Et nous pouvons progresser vers la solution grâce à l'affectation :
\begin{equation*} x \gets x \cup s(x) \end{equation*}Mais, sous quelle condition devons-nous sortir de la boucle ? Nous remarquons :
\begin{equation*} s(x) \subseteq x \quad \Rightarrow \quad a(x) = x \end{equation*}En effet :
\begin{equation*} \begin{aligned} & a(x) = x \\ \equiv \quad &\{\text{déf. de } a : a(x) = x \cup a(s(x))\} \\ & a(x) = a(x) \cap a(s(x)) \\ \equiv \quad &\{\text{algèbre}\} \\ & a(s(x)) \subseteq a(x) \\ \equiv \quad &\{\text{hyp. } s(x) \subseteq x \text{ et } a \subseteq b \Rightarrow a(a) \subseteq a(b)\} \\ & true \end{aligned} \end{equation*}En effet :
\begin{equation*} \begin{aligned} & a(a) \subseteq a(b) \\ \equiv \quad &\{\text{déf. de } a\} \\ & a \cup a(s(a)) \subseteq b \cup a(s(b)) \\ \Leftarrow \quad &\{\text{hyp. } a \subseteq b\} \\ & a(s(a)) \subseteq a(s(b)) \\ \equiv \quad &\{\text{réc.}\} \\ & true \end{aligned} \end{equation*}Nous avons donc montré que :
\begin{equation*} P0 \; \wedge \; (s(x) \subseteq x) \; \Rightarrow \; R \end{equation*}D'où une première version du programme :

Figure 2: Première version de l'algorithme Atteignable
1.1.2 Optimisation
Le programme que nous avons dérivé peut calculer plusieurs fois les successeurs d'un même nœud. Nous modifions l'invariant pour distinguer les nœuds dont les successeurs nous sont déjà connus (notés \(x\) et que nous appellerons aussi les nœuds noirs) de ceux déjà rencontrés mais dont les successeurs nous sont encore inconnus (notés \(y\) et que nous appellerons aussi les nœuds gris). Nous appellerons les nœuds encore non considérés : les nœuds blancs.
\begin{equation*} P1 : \quad a(\{v\}) = a(x \cup y) \;\; \wedge \;\; x \cap y = \emptyset \;\; \wedge \;\; s(x) \subseteq (x \cup y) \end{equation*}Ce qui nous dirige vers le nouveau programme optimisé :

Figure 3: Version optimisée de l'algorithme Atteignable
Le programme termine-t-il ? Le nombre de nœuds qui ne sont pas dans \(x\) est au moins \(0\). A chaque itération, ce nombre décroît du nombre de nœuds de \(y\) ( car \(x \cap y = \emptyset\) ). Or le nombre de nœuds de \(y\) est strictement positif à cause de la clause garde de la boucle ( \(y \neq \emptyset\) ). Ainsi, nous avons isolé une fonction monotone stricte et bornée ("bound function") qui prouve la terminaison du programme.
Nous savons que ce programme est correct car nous l'avons dérivé à partir de sa spécification.
1.2 Implémentation C++
Nous proposons maintenant une implémentation du programme qui, étant donné un graphe orienté G et un nœud v de ce graphe, calcule l'ensemble des nœuds atteignables à partir de v.
Chaque nœud porte une valeur entière et une liste de voisins directs.
struct node { int val; vector<node*> nei; };
Nous calculons la fermeture de la relation de voisinage.
set<node*> a( node* src ) { set<node*> x; set<node*> y; y.insert(src); while( !y.empty() ) { set<node*>::iterator u = y.begin(); for( node* n : (*u)->nei ) { if( (x.end() == x.find(n)) && (y.end() == y.find(n)) ) { y.insert(n); } } x.insert(*u); y.erase(u); } return x; }
Nous avons par exemple :
\begin{equation*} a(\&n4) = 6 ; 5 ; 4 ; 3 ; 2 ; \end{equation*}2 Recherche en largeur (breadth-first search)
2.1 Structure FIFO
En utilisant pour \(y\) (la structure qui contient les nœuds rencontrés mais dont les successeurs n'ont pas encore été calculés) une structure de file FIFO (First In First Out) au lieu d'un ensemble, nous obtenons le programme de recherche en largeur dans un graphe.
typedef function<void(node*)> Visitor; void breadth( node* src, Visitor f ) { set<node*> x; queue<node*> y; y.push(src); x.insert(src); while( !y.empty() ) { node* u = y.front(); y.pop(); f(u); for( node* n : u->nei ) { if( x.end() == x.find(n)){ y.push(n); x.insert(n); } } } }
Ci-dessous un résultat possible pour un parcours en largeur sur l'exemple précédent en partant du nœud 1 comme source. Nous utilisons un visiteur trivial :
Visitor visit = [](node* v){ cout << v->val << " ; "; };
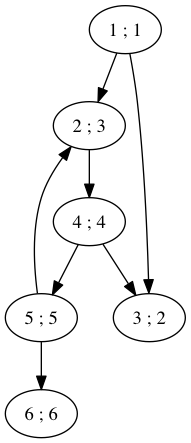
Figure 4: Graphe pour illustrer l'algorithme de parcours en largeur
2.2 Calcul des plus courts chemins
L'algorithme de recherche en largeur permet de trouver les plus courts chemins d'un nœud source aux autres nœuds du graphe dans le cas d'un graphe orienté pour lequel les arêtes ont toutes le même coût (ou poids) :
void findDistances( node* src, map<node*,size_t>* distances ) { function<size_t(node*)> distance = [distances]( node* v ) { map<node*,size_t>::iterator distIt = distances->find(v); if( distances->end() == distIt ) { return numeric_limits<size_t>::max(); } return distIt->second; }; Visitor visit = [distances, distance]( node* v ) { if( distances->empty() ) (*distances)[v] = 0; for (node* n : v->nei) { size_t vDist = distance(v); size_t nDist = distance(n); (*distances)[n] = min( nDist, 1 + vDist ); } }; breadth(src, visit); }
Sur l'exemple, en prenant pour source le nœud 1, nous trouvons :
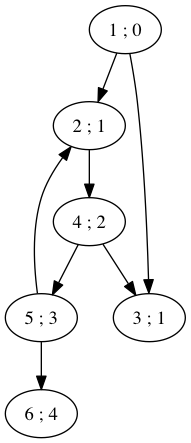
Figure 5: Graphe pour illustrer l'utilisation du parcours en largeur pour la découverte des plus courts chemins
3 Recherche en profondeur (depth-first search)
3.1 Structure LIFO (Last In First Out)
En utilisant pour \(y\) (la structure qui contient les nœuds rencontrés mais dont les successeurs ne sont pas encore calculés, les nœuds gris) une structure de pile LIFO (Last In First Out) au lieu d'un ensemble, nous obtenons le programme de recherche en profondeur dans un graphe.
typedef function<void(node*)> Visitor; void depth( node* src, Visitor f ) { set<node*> x; stack< pair< node* , vector<node*>::iterator > > y; y.push( { src, src->nei.begin() } ); x.insert(src); while( !y.empty() ) { node* u = y.top().first; vector<node*>::iterator n = y.top().second; if( n != u->nei.end() ) { node* next = *n; ++n; if( x.end() == x.find(next) ) { y.push( { next, next->nei.begin() } ); x.insert(next); } continue; } f(u); y.pop(); } }
Ci-dessous un résultat possible d'un parcours en profondeur sur l'exemple précédent en partant du nœud 1 comme source.
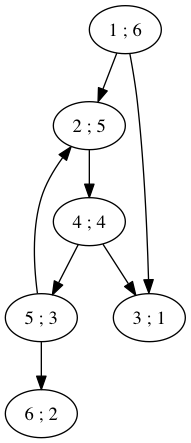
Figure 6: Graphe pour illustrer l'algorithme de parcours en profondeur
3.2 Version récursive
La recherche en profondeur s'écrit plus naturellement sous une forme récursive :
typedef function<void(node*)> Visitor; void depthrec( node* src, Visitor f, set<node*>* x ) { (*x).insert(src); for( node* n : src->nei ) { if( (*x).end() == (*x).find(n) ) { depthrec( n, f, x ); } } f(src); } void depth( node* src, Visitor f ) { set<node*> x; depthrec(src, f, &x); }
4 Plus court chemin sur un graphe aux arêtes étiquetées positivement (Dijkstra)
4.1 Principe de l'algorithme
Nous considérons un graphe dont chaque arête est étiquetée avec un nombre positif ou nul. Il s'agit de calculer pour chaque nœud du graphe sa plus courte distance à un nœud \(v\) fixé. La plus courte distance entre deux nœuds est la longueur du plus court chemin entre ces deux nœuds.
L'ensemble des nœuds noirs est l'ensemble des nœuds pour lesquels la plus courte distance à \(v\) a été établie. Un plus court chemin ne visite que des nœuds noirs.
L'ensemble des nœuds gris est l'ensemble des nœuds pour lesquels la longueur d'un chemin y menant depuis \(v\) a été établie, mais cette longueur n'est pas nécessairement minimale. Par contre, c'est la longueur minimale sur l'ensemble des chemins qui n'ont que des nœuds noirs entre \(v\) et ce nœud gris.
Au sujet des nœuds blancs, nous ne savons rien… sinon que tout chemin depuis \(v\) jusqu'à un nœud blanc doit d'abord passer par un nœud gris.
On note \(d[u]\) la distance associée à un nœud noir ou gris.
Comment choisir le prochain nœud gris que nous ferons passer à noir ?
Nous montrons que nous pouvons choisir un nœud gris \(u\) dont la distance depuis \(v\), notée \(d[u]\), (et qui est la longueur d'un chemin ne passant que par des nœuds noirs) est minimale parmi l'ensemble des nœuds gris.
Considérons un chemin quelconque de \(v\) à \(u\) et notons sa longueur \(l\). Ce chemin peut contenir d'autres nœuds gris et même des nœuds blancs.
Puisque \(v\) est noir et \(u\) est gris, à un moment donné ce chemin quitte la région noire.
Soit \(g\) le premier nœud non-noir (c-à-d gris) de ce chemin.
\(g\) peut être égal à \(u\) ou ne pas être égal à \(u\).
Puisque \(u\) a été choisi pour minimiser \(d[u]\), nous avons : \(d[u] \leq d[g]\).
Puisque la distance de \(g\) à \(u\) est positive ou nulle, nous avons : \(d[g] \leq l\).
D'où : \(d[u] \leq l\). Donc ce chemin est au moins aussi long que celui dont la découverte avait mené à la mémorisation de la valeur actuelle \(d[u]\).
Donc la longueur du plus court chemin de \(v\) à \(u\) est \(d[u]\), et le nœud \(u\) peut être coloré en noir.
Tous les successeurs blancs de \(u\) sont colorés en gris, et une distance est mémorisée pour chacun d'entre eux, faite de la plus courte distance de \(v\) à \(u\) (\(d[u]\) ) plus la distance de \(u\) à son successeur.
Tous les successeurs gris de \(u\) restent gris, mais la distance qui leur est associée peut être réduite (si le chemin qui passe par u est plus court).
Pour les successeurs noirs de \(u\), il n'y a rien à faire.
D'où l'algorithme suivant :

Figure 7: Algorithme de Dijkstra pour la recherche d'un plus court chemin
4.2 Implémentation
La liste d'adjacence d'un noeud contient maintenant les poids des arêtes qui permettent de rejoindre les voisins de ce noeud :
struct node { int val; vector< pair< int, node* > > nei; };
L'implémentation de l'algorithme suit d'assez près le pseudo-code de notre dérivation. La différence principale réside dans l'utilisation d'une file de priorité, et dans le maintient d'une structure map< node*, node* > parent qui permet de reconstruire le chemin une fois la destination atteinte.
void dijkstra( node* src, node* target, list<node*>* r ) { map< node*, node* > parent; parent[src] = src; map< node*, int> d; d[src] = 0; set<node*> x; priority_queue< pair< int, node* > , vector< pair< int, node* > >, greater< pair< int, node* > > > y; y.push({0, src}); x.insert(src); function<int(node*)> dist = [d]( node* v ) { map< node*, int >::const_iterator it = d.find(v); if( d.end() == it ) { return numeric_limits<int>::max(); } return it->second; }; while( !y.empty() ) { node* u = y.top().second; if( target == u ) { r->clear(); while( u != src ) { r->push_front(u); u = parent[u]; } r->push_front(src); return; } x.insert(u); y.pop(); for( pair< int, node* > n : u->nei ) { if( x.end() != x.find(n.second) ) { continue; } // We don't take into account as a special case the situation of // n already an element of y. // Indeed, the basic STL priority queue doesn't have // an increaseKey operation. // Therefore, we tolerate duplicates... // But really, we may prefer using a "better" structure... if( dist(n.second) > d[u] + n.first ) { d[n.second] = d[u] + n.first; parent[n.second] = u; y.push( { d[n.second], n.second } ); } } } }
4.3 Exemple
Nous mettons à jour notre petit exemple de graphe en ajoutant des poids aux arêtes :
struct node n1; n1.val = 1; struct node n2; n2.val = 2; struct node n3; n3.val = 3; struct node n4; n4.val = 4; struct node n5; n5.val = 5; struct node n6; n6.val = 6; n1.nei.insert(n1.nei.begin(), { 1, &n2 }); n1.nei.insert(n1.nei.begin(), { 4, &n3 }); n2.nei.insert(n2.nei.begin(), { 1, &n4 }); n2.nei.insert(n2.nei.begin(), { 2, &n5 }); n4.nei.insert(n4.nei.begin(), { 1, &n3 }); n4.nei.insert(n4.nei.begin(), { 2, &n5 }); n5.nei.insert(n5.nei.begin(), { 1, &n6 }); n6.nei.insert(n6.nei.begin(), { 1, &n2 });
Nous testons, sur cet exemple, l'algorithme de Dijkstra pour la recherche d'un plus court chemin.
<<dijkstra-include>> <<dijkstra-struct-node>> <<dijkstra-algo>> int main() { <<dijkstra-example>> list<node*> r; dijkstra(&n1, &n3, &r); for( list<node*>::iterator it = r.begin() ; it != r.end() ; it++ ) { cout << (*it)->val << " ; "; } cout << endl; return 0; }
Le résultat de la recherche du plus court chemin de 1 vers 3 donne bien :
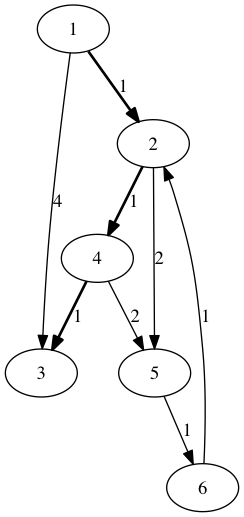
Figure 8: Graphe pour illustrer l'algorithme de Dijkstra pour la recherche d'un plus court chemin
5 Plus court chemin en présence d'information contextuelle
Comment améliorer la recherche d'un plus court chemin entre un nœud source \(s\) et un nœud cible \(t\) quand nous possédons pour tout nœud \(u\) du graphe une estimation \(h(u)\) de la distance séparant \(u\) de la cible ?
5.1 La notion de fonction heuristique
La fonction \(h\) est appelée fonction heuristique.
Déf. Une heuristique \(h\) est admissible si pour tout nœud \(u\), \(h(u)\) est une borne inférieure de la plus courte distance séparant \(u\) de la cible \(t\), i.e. \(h(u) \leq \delta(u,t)\) (avec \(\delta(u,t)\) désignant la longueur d'un chemin optimal entre \(u\) et \(t\) ).
Déf. Une heuristique \(h\) est consistante si pour toute arête \(e = (u,v)\) nous avons \(h(u) \leq h(v) + w(u,v)\) (avec \(w(u,v)\) le poids de l'arête \((u,v)\) ).
Déf. Soient \((u_0,\dots,u_k)\) un chemin et \(g(u_i)\) le coût du chemin \((u_0,\dots,u_i)\). Nous posons \(f(u_i) = g(u_i) + h(u_i)\). Une heuristique \(h\) est monotone si pour tout \(j>i, \; 0 \leq i, \; j \leq k\) nous avons \(f(u_j) \geq f(u_i)\). C'est-à-dire que l'estimation du poids total d'un chemin ne décroît pas lors du passage d'un nœud à ses successeurs.
Nous remarquons que consistance et monotonicité sont deux propriétés équivalentes. En effet, pour deux nœuds adjacents \(u_{i-1}\) et \(u_i\) sur un chemin \((u_0,\dots,u_k)\), nous avons :
\begin{equation*} \begin{aligned} & f(u_i) \\ = \quad &\{\text{Déf. de } f\} \\ & g(u_i) + h(u_i) \\ = \quad &\{\text{Déf. du coût d'un chemin}\} \\ & g(u_{i-1}) + w(u_{i-1}, u_i) + h(u_i) \\ \geq \quad &\{\text{Déf. de la consistance}\} \\ & g(u_{i-1}) + h(u_{i-1}) \\ = \quad &\{\text{Déf. de } f\} \\ & f(u_{i-1}) \end{aligned} \end{equation*}Aussi, une heuristique consistante est admissible (la réciproque n'est pas vraie). En effet, si \(h\) est consistante, pour toute arête \((u,v)\) nous avons \(h(u) - h(v) \leq w(u,v)\). Soit un chemin quelconque \(p = (v_0 = u,\dots,v_k = t)\), nous avons :
\begin{equation*} \begin{aligned} & w(p) \\ = \quad &\{\text{Déf. du poids d'un chemin}\} \\ & \sum_{i=0}^{k-1} w(v_i, v_{i+1}) \\ \geq \quad &\{\text{Consistance de } h\} \\ & \sum_{i=0}^{k-1} h(v_i) - h(v_{i+1}) \\ = \quad &\{\text{Arithmétique}\} \\ & h(u) - h(t) \\ = \quad &\{t \text{ est la cible}\} \\ & h(u) \end{aligned} \end{equation*}En particulier, dans le cas d'un plus court chemin : \(h(u) \leq \delta(u,t)\).
5.2 L'algorithme A*
L'algorithme A* est un exemple d'amélioration de l'algorithme de Dijkstra grâce à l'utilisation d'une fonction heuristique. A* associe à un nœud \(u\) du graphe la valeur :
\begin{equation*} f(u) = g(u) + h(u) \end{equation*}où \(g(u)\) est le poids optimal actuellement connu pour un chemin menant de \(s\) à \(u\), et \(h(u)\) est une heuristique admissible (i.e., une borne inférieure de la distance séparant \(u\) de la cible \(t\) ).
Nous remarquons que pour un nœud \(u\) gris minimal (au sens de \(f(u)\) ), nous avons pour tout successeur \(v\) de \(u\) :
\begin{equation*} \begin{aligned} & f(v) \\ = \quad &\{\text{Déf. de } f\} \\ & g(v) + h(v) \\ = \quad &\{v \text{ est un nœud gris minimal}\} \\ & g(u) + w(u,v) + h(v) \\ = \quad &\{\text{Arithmétique (du vieux vin dans une nouvelle bouteille ?)}\} \\ & g(u) + h(u) + w(u,v) - h(u) + h(v) \\ = \quad &\{\text{Déf. de } f\} \\ & f(u) + w(u,v) - h(u) + h(v) \end{aligned} \end{equation*}Ainsi, l'algorithme A* correspond exactement à l'algorithme de Dijkstra avec la repondération suivante :
\begin{equation*} \hat{w}(u,v) = w(u,v) - h(u) + h(v) \end{equation*}Si l'heuristique \(h\) est monotone alors tous les poids restent positifs et la preuve de correction de Dijkstra s'applique !
De plus, nous allons montrer que, dans le cas d'une heuristique monotone, il n'existe pas d'algorithme \(A\) qui trouve la solution optimale en explorant moins de nœuds que \(A^*\). Soit \(f^* = \delta(s,t)\) le coût de la solution optimale. Nous montrons que tout algorithme optimal (i.e., qui trouvera toujours la solution optimale) doit visiter tous les nœuds \(u\) pour lesquels \(\delta(s,u) < f^*\).
Travaillons par l'absurde en supposant qu'il existe un algorithme \(A\) qui trouve une solution optimale \(p_t\) (i.e., avec \(w(p_t) = f^*\) ) en ne visitant pas un nœud \(u\) pour lequel \(\delta(s,u) < f^*\). Montrons qu'il peut alors exister un autre chemin \(q\) avec \(w(q) < f^*\) qui n'est pas trouvé par A. Soit \(q_u\) le chemin tel que \(w(q_u) = \delta(s,u)\). Mettons qu'il existe une arête \((u,t)\) de poids \(0\) (i.e., \(w(u,t) = 0\) ). Puisque le voisinage de \(u\) n'a pas été exploré par \(A\), ce dernier ne peut pas savoir que l'arête \((u,t)\) existe. Soit le chemin \(q = (q_u,t)\). Nous avons : \(w(q) = w(q_u) + w(u,t) = \delta(s,u) < f^*\).
5.3 Comparer des heuristiques
Plus une heuristique \(h(u)\) est proche de la valeur optimale \(\delta(u,t)\) plus elle est informée. Plus une heuristique est informée, mieux elle minimise la taille de l'espace exploré, mais en général elle est également plus coûteuse en temps de calcul qu'une heuristique moins informée.
6 Exemple sur le jeu de taquin de taille 8
6.1 Contexte
Prenons l'exemple simple du 8-puzzle dont on rappelle ci-dessous le voisinage :
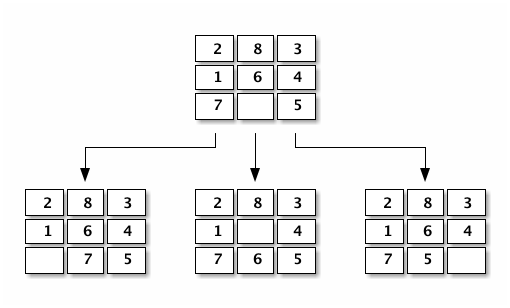
Figure 9: Quatre configurations voisines pour le 8-puzzle
6.2 Heuristiques
Voici quelques exemples d'heuristiques ordonnées par degré d'information :
- nombre de chiffres mal placés
- somme des distances (de manhattan) des chiffres à leurs positions d'origine
- prise en compte des échanges entre cases voisines
- …
6.3 Implémentation
Nous commençons par définir le type d'un nœud et d'une fonction heuristique :
typedef vector<int> Board; typedef function<int( const Board& pos )> Heuristic;
Nous introduisons une fonction accessoire pour calculer la taille du côté d'une grille.
int side( const Board& b ) { double y = sqrt( b.size() ); int x = y; return x; }
Puis nous définissons trois heuristiques :
int breadth( const Board& b ) { return 0; } int nbmis( const Board& b ) { int d = 0; for( int i = 0 ; i < b.size() ; i++ ) { if( b[i] != i ) d++; } return d; } int manh( const Board& b ) { int d = 0; int s = side(b); for( int i = 0 ; i < b.size() ; i++ ) { d += abs( i / s - b[i] / s ) + abs( i % s - b[i] % s ); } return d; }
La fonction ok indique si la configuration finale est atteinte :
bool ok( const Board& b ) { return (nbmis(b) == 0); }
Nous adaptons l'algorithme \(A^*\) (i.e. Dijkstra…) à ce contexte :
void astar( const Board& src, Heuristic h, list<Board> *r, int *nbiter ) { <<taquin-astar-init>> <<taquin-astar-dist>> while( !y.empty() ) { Board u = y.top().second; (*nbiter)++; if( ok(u) ) { <<taquin-astar-stop>> return; } x.insert(u); y.pop(); <<taquin-astar-neighbors>> for( Board n : neighbors ) { <<taquin-astar-update>> } } }
Nous utilisons une fonction locale pour retourner la plus petite distance actuellement connue pour rejoindre un nœud donné. Dans le cas d'un nœud pour lequel aucune estimation de distance n'a pour l'instant été proposée, cette fonction retourne l'infini :
function<int(const Board&)> dist = [d]( const Board& b ) { map< Board , int >::const_iterator it = d.find(b); if( d.end() == it ) { return numeric_limits<int>::max(); } return it->second; };
La mise à jour de la file de priorité ne pose pas de difficulté. Nous utilisons la repondération de l'algorithme \(A^*\) avec l'heuristique h et avec un coût de base de \(1\) entre deux configurations voisines :
if( x.end() != x.find(n) ) { continue; } int new_cost = d[u] + 1 - h(u) + h(n); if( dist(n) > new_cost ) { d[n] = new_cost; parent[n] = u; y.push( { d[n] , n } ); }
Quand une solution optimale u est trouvée, nous reconstruisons dans la liste r le chemin y menant :
r->clear();
while( u != src )
{
r->push_front(u);
u = parent[u];
}
r->push_front(src);
Pour calculer les voisins neighbors de u, nous utilisons quelques petites astuces algébriques :
neighbors.clear(); int pos0 = find( u.begin(), u.end(), 0 ) - u.begin(); if( (pos0 + 1) < u.size() && ((pos0 + 1) % s) != 0 ) { Board n = u; swap( n[pos0] , n[pos0 + 1] ); neighbors.push_back(n); } if( (pos0 - 1) >= 0 && ((pos0 - 1) % s) != (s-1) ) { Board n = u; swap( n[pos0] , n[pos0 - 1] ); neighbors.push_back(n); } if( (pos0 + s) < u.size() ) { Board n = u; swap( n[pos0] , n[pos0 + s] ); neighbors.push_back(n); } if( (pos0 - s) >= 0 ) { Board n = u; swap( n[pos0] , n[pos0 - s] ); neighbors.push_back(n); }
L'initialisation ne pose pas de difficulté, sinon qu'avec la nouvelle pondération de \(A^*\) il faut penser à initialiser le poids de la source avec la valeur de l'heuristique h(src) :
int s = side(src); map< Board , Board > parent; parent[src] = src; map< Board , int > d; d[src] = h(src); set< Board > x; priority_queue< pair< int , Board >, vector< pair< int, Board > >, greater< pair< int, Board > > > y; y.push( { d[src], src } ); x.insert(src); vector<Board> neighbors; (*nbiter) = 0;
Nous introduisons une fonction accessoire pour afficher une grille :
void print( const Board& b ) { int s = side(b); for( int i = 0 ; i < b.size() ; i++ ) { if( i % s == 0 ) cout << endl; cout << setw(2) << setfill('0') << b[i] << " , "; } cout << endl; }
Nous testons le programme sur une petite grille de côté \(8\) :
<<taquin-include>> <<taquin-types>> <<taquin-side>> <<taquin-heuristics>> <<taquin-ok>> <<taquin-print>> <<taquin-astar>> int main() { Board b = {4,8,3,2,0,7,6,5,1}; list<Board> r; int nbiter = 0; astar(b, breadth, &r, &nbiter); cout << "Heuristic breadth:" << endl; cout << "nb moves: " << r.size() << endl; cout << "nb nodes explored: " << nbiter << endl; for( list<Board>::iterator it = r.begin() ; it != r.end() ; it++ ) { print( (*it) ); } r.clear(); astar(b, nbmis, &r, &nbiter); cout << "Heuristic nbmis:" << endl; cout << "nb moves: " << r.size() << endl; cout << "nb nodes explored: " << nbiter << endl; for( list<Board>::iterator it = r.begin() ; it != r.end() ; it++ ) { print( (*it) ); } r.clear(); astar(b, manh, &r, &nbiter); cout << "Heuristic manh:" << endl; cout << "nb moves: " << r.size() << endl; cout << "nb nodes explored: " << nbiter << endl; for( list<Board>::iterator it = r.begin() ; it != r.end() ; it++ ) { print( (*it) ); } return 0; }
6.4 Résultats
- heuristique
breadth- 21 coups
- 65726 nœuds explorés
- heuristique
nbmis- 21 coups
- 3045 nœuds explorés
- heuristique
manh- 21 coups
- 386 nœuds explorés
7 Exemple sur le jeu de taquin de taille 15
<<taquin-include>> <<taquin-types>> <<taquin-side>> <<taquin-heuristics>> <<taquin-ok>> <<taquin-print>> <<taquin-astar>> int main() { Board b = {11,5,12,14,15,2,0,9,13,7,6,1,3,10,4,8}; list<Board> r; int nbiter = 0; astar(b, manh, &r, &nbiter); cout << "Heuristic manh:" << endl; cout << "nb moves: " << r.size() << endl; cout << "nb nodes explored: " << nbiter << endl; return 0; }
Sur cette instance, nous n'arrivons pas à trouver une solution… L'algorithme A* en tant que variante de la recherche en largeur est gourmand en mémoire (toutes les configurations de coût inférieur à la solution optimale sont mémorisées).
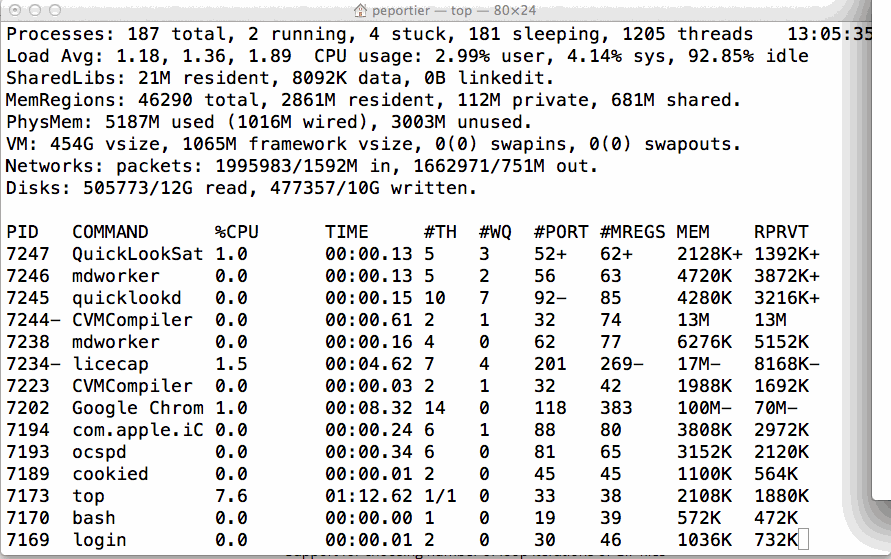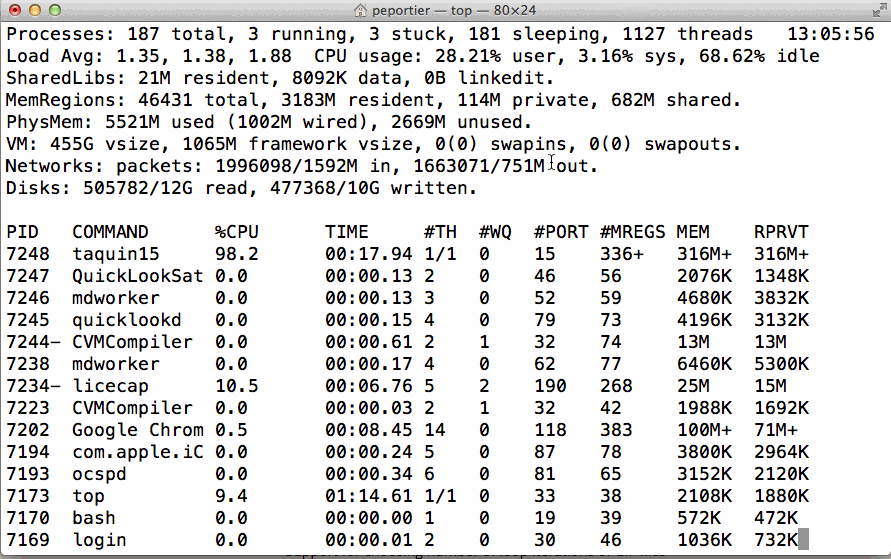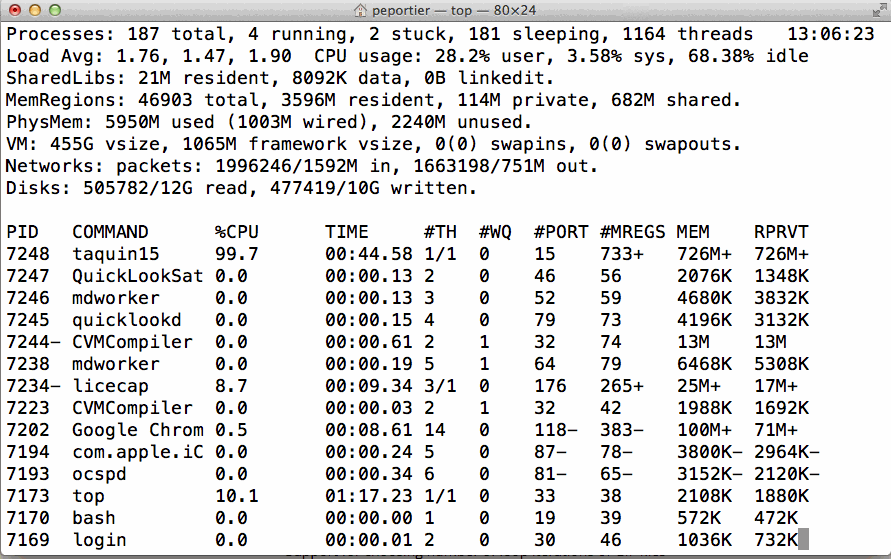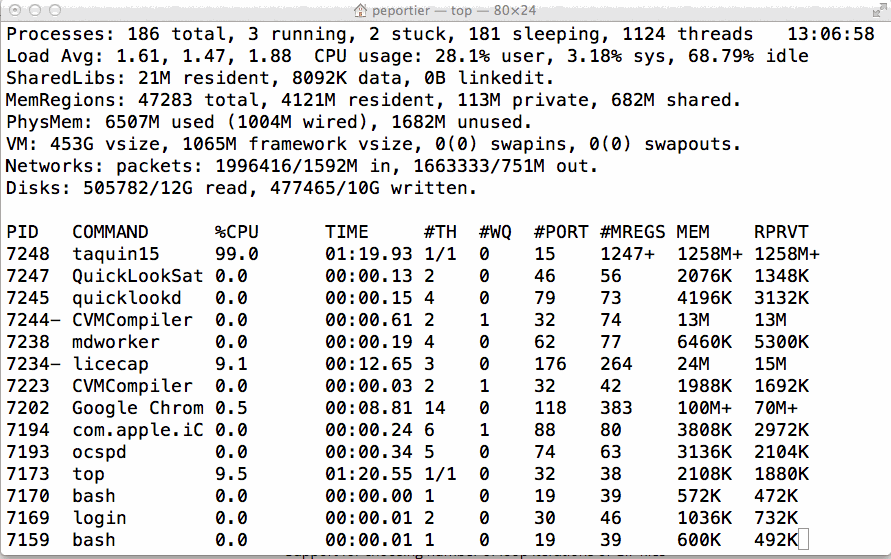
Figure 10: Illustration de la consommation mémoire pour l'algorithme A* sur le taquin15
8 Approfondissement itéré (iterative deepening)
Il s'agit de faire un parcours en profondeur jusqu'à une profondeur maximale \(n\). Si aucune solution n'est trouvée, une nouvelle recherche est lancée jusqu'à une profondeur maximale \(n+1\). Etc.

Figure 11: Recherche en profondeur avec approfondissement itéré
Soit \(N_b(d)\) le nombre de nœuds d'un espace d'états structuré en arbre enraciné de profondeur \(d\) et de facteur de branchement \(b\) (i.e., chaque nœud qui n'est pas une feuille possède \(b\) fils). Nous avons :
\begin{equation*} N_b(d) = \sum_{i=0}^{d} b^i = \frac{b^{d+1} - 1}{b - 1} \end{equation*}Ainsi :
\begin{equation*} \begin{aligned} & \sum_{d=1}^{d_{max}-1} N_b(d) \\ = \quad & \sum_{d=1}^{d_{max}-1} \frac{b^{d+1}-1}{b-1} \\ = \quad & \frac{1}{b-1} \left(\left( \sum_{d=1}^{d_{max}-1} b^{d+1} \right) - d_{max} + 1 \right) \\ = \quad & \frac{1}{b-1} \left(\left( \sum_{d=2}^{d_{max}} b^d \right) - d_{max} + 1 \right) \\ = \quad & \frac{1}{b-1} \left( \frac{b^{d_{max}+1} - 1}{b - 1} - 1 - b - d_{max} + 1 \right) \\ \approx \quad & \frac{1}{b-1} \left( \frac{b^{d_{max}+1} - 1}{b - 1}\right) \\ = \quad & \frac{1}{b-1} N_b(d_{max}) \end{aligned} \end{equation*}Donc, à partir d'un facteur de branchement \(b > 2\), il y a moins de nœuds dans la somme de tous les arbres excepté le dernier que de nœuds dans le dernier arbre.
9 Approfondissement itéré pour l'algorithme A* (IDA*)

Figure 12: Algorithme A* avec approfondissement itéré
Avec IDA*, nous pouvons résoudre le 15-puzzle. Comment résoudre le 24-puzzle ?