
Lessons:
3. Constructivist epistemology

Home » 6. Cognitive architecture » 64. Formalism
The architecture in Figure 62 raises the issue of localizing interactions in space, and of updating spatial memory as the agent moves. For example, if the agent touched an object to the right, then turned left, the agent must update its spatial memory to keep track of the fact that the touch right interaction had been enacted in a position that is now behind the agent.
To address this issue, we designed the spatio-sequential policy coupling shown in Figure 63, as an extension of the RI model introduced in Figure 51.
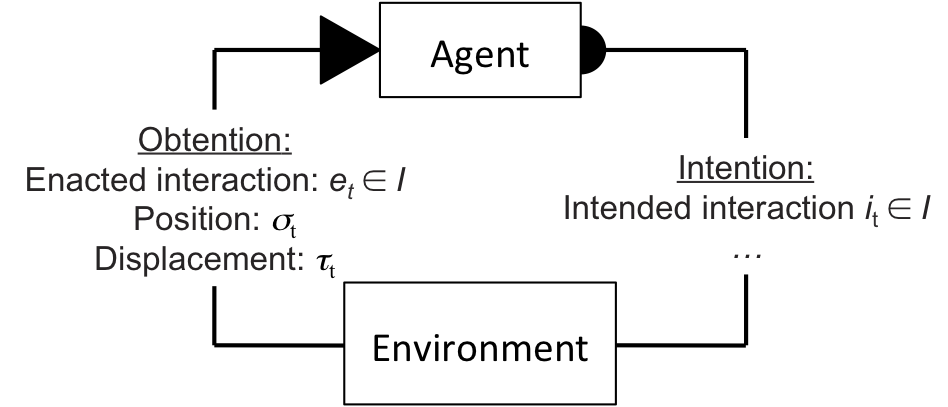
Figure 64: Spatio-sequential policy coupling. The agent sends a data structure called Intention to the environment, containing the intended interaction it. In return, the agent receives a data structure called Obtention, containing the enacted interaction et, the enacted interaction's position relative to the agent σt, and the geometrical transformation resulting from the agent's displacement τt.
The spatio-sequential policy coupling extends the RI model by adding information σt and τt to provide the agent with spatial information related to the enaction of et.
σt specifies a point in the space surrounding the agent where et can be approximately situated. In a two-dimensional environment, σt ∈ ℝ2 represents the Cartesian coordinates of this point in the agent's egocentric referential.
τt specifies a geometrical transformation that approximately represents the agent's movement in space resulting from the enaction of et. In a two-dimensional environment, τt = (θt, ρt) with θt ∈ ℝ being the angle of rotation of the environment relative to the agent, and ρt ∈ ℝ2 the two dimensional vector of translation of the environment relative to the agent.
The intuition for σt is that the agent has sensory information available to it that helps it situate an interaction in space. For example, humans are known to use eye convergence, kinesthetic information, and interaural time delay (among other forms of sensory information) to infer the spatial origin of their visual, tactile, and auditory experiences.
The intuition for τt is that the agent has sensory information available that helps it keep track of its own displacements in space. Humans are known to use vestibular and optic flow information to realize such tracking.
In videos 63-1 and 63-2, these sensors were simulated by a function that directly passed σt and τt from the environment to the agent.
In robots, σt and τt can be derived from spatial sensors such as telemeters and accelerometers. The robot, however, would need to calibrate its spatial sensors to generate σt and τt with enough precision. If the spatial sensors cannot be satisfactorily calibrated, then the agent's spatial memory would need to implement more complex geometrical operations than simple affine transformations. We still need to investigate how a robot can autonomously calibrate its spatial sensors, or how spatial memory can implement more complex geometrical operations to deal with uncalibrated sensors.
Notably, the policy coupling in Figure 64 also opens the way to including more information in the Intention data structure. This data structure could include more than one intended interaction on each interaction cycle, allowing the robot to control different body parts simultaneously. For example, a two-wheel robot could control each of its wheels separately, by sending an intended interaction associated with each wheel. This would allow generating more sophisticated behaviors than in the experiment of Video 53, in which the move forward and turn interactions controlled the two wheels simultaneously in a predefined manner.
The Intention data structure could also include spatial information allowing the agent to specify the position in which it intends to enact an interaction. This position would correspond to an intended σt, identical to the obtained σt in the Obtention data structure. For example, we imagine a different implementation of the experiment in Video 63-1, in which the agent could choose where it intends to enact the touching interaction by specifying its intended position (e.g., [1,0]: (front), [0,1]: (left), etc.).
See public discussions about this page or start a new discussion by clicking on the Google+ Share button. Please type the #IDEALMOOC064 hashtag in your post: