
 Home page
Home page Researches
Researches Publications
Publications Teaching
Teaching Supervised Thesis
Supervised Thesis CV
CV Contacts
Contacts Links
Links | Publications |  |
Books International Journals International Conferences Book Chapters Thesis Editors Softwares
Format: Sort by: Display:
| Books |
| [B1] Combinatorial Maps: Efficient Data Structures for Computer Graphics and Image Processing Damiand G., Lienhardt P. A K Peters/CRC Press, September 2014 Abstract: A Versatile Framework for Handling Subdivided Geometric Objects.
Combinatorial Maps: Efficient Data Structures for Computer Graphics and Image Processing gathers important ideas related to combinatorial maps and explains how the maps are applied in geometric modeling and image processing. It focuses on two subclasses of combinatorial maps: n-Gmaps and n-maps.
Suitable for researchers and graduate students in geometric modeling, computational and discrete geometry, computer graphics, and image processing and analysis, the book presents the data structures, operations, and algorithms that are useful in handling subdivided geometric objects. It shows how to study data structures for the explicit representation of subdivided geometric objects and describes operations for handling the structures. The book also illustrates results of the design of data structures and operations. |   |  |
| International Journals |
| [J27] Query-replace operations for topologically controlled 3D mesh editing Damiand G., Nivoliers V. Computers & Graphics (C&G), Volume 106, pages 187-199, August 2022 Abstract: We propose a generic framework to describe modifications on 3D objects (surfaces and volumes) based on a query and replace mechanism. These modifications are described in terms of rewriting rules: a set of patterns is provided, each one defining a possible replacement. The patterns are expressed using 3D combinatorial maps, ensuring the global topological validity of the transformed mesh. At the core of the framework, we use topological signatures to efficiently query and match patterns on the input. Our formalism can generically describe many different transformations like subdivision, smoothing, topological correction, or remeshing. Its interest is twofold. It provides an easy implementation for such operations, especially when many cases arise: we provide an example with over 300 cases. It is also able to detect corner cases that were not provided and are required to ensure the topological correctness of the output. |    |  |
| [J26] Hierarchical mesh-to-points as-rigid-as-possible registration Bourquat P., Coeurjolly D., Damiand G., Dupont F. Computers & Graphics (C&G), Volume 102, pages 320-328, February 2022 Abstract: Surface registration is a fundamental problem in computer graphics and computer-aided design. The problem consists in finding a deformation from one surface to another that preserves some properties. For instance, in our inverse engineering context, we aim at finding the best, as isometric as possible, map between an input triangular model, and a large point cloud acquired on the actual mechanical part being processed. Existing solutions are not able to handle very large models with a good level of precision. We propose a method which is accurate and fast. Our solution combines an efficient iterative energy minimization scheme on a hierarchical decomposition of the problem geometry. Our experiments show that we obtain a fast and efficient algorithm compared to the state-of-the art method, while keeping its numerical accuracy. |    |  |
| [J25] Stripped halfedge data structure for parallel computation of arrangements of segments Damiand G., Coeurjolly D., Bourquat P. The Visual Computer, Volume 37, Number 9, pages 2461-2472, September 2021 Abstract: Computing an arrangement of segments with some geometrical and topological guarantees is a critical step in many geometry processing applications. In this paper, we propose a method to efficiently compute arrangements of segments using a strip-based data structure. Thanks to this new data structure, the arrangement computation algorithm can easily be parallelized as the per strip computations are independent. Another interest of our approach is that we can propose an out-of-core and streamed construction for large datasets, while keeping a low memory footprint. We prove the correctness of our structure and provide a complete comparative evaluation with respect to state-of-the-art demonstrating the interest of our construction for the computation of an exact arrangement. |    | 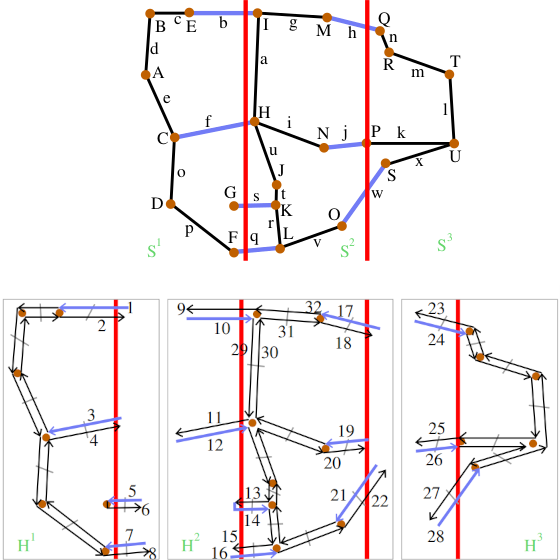 |
| [J24] Hybrid 3D mass-spring system for simulation of isotropic materials with any Poisson’s ratio Golec K., Palierne J.-F., Zara F., Nicolle S., Damiand G. The Visual Computer, Volume 36, Number 4, pages 809-825, April 2020 Abstract: Mass-Spring Systems (MSS) simulating elastic materials obey constraints known in elasticity as the Cauchy relations, restricting the Poisson ratio of isotropic systems to be exactly nu = 1/4. We remind that this limitation is intrinsic to centrosymmetric spring systems (where each node is a center of symmetry), forbidding them for instance to simulate incompressible materials (with nu = 1/2). To overcome this restriction, we propose to supplement the spring deformation energy with an energy depending on the volume only, insensitive to change of shape, permitting MSS to simulate any real isotropic materials. In addition, the freedom in choosing the spring constants realizing a given elastic behavior allows to manage instabilities. The proposed hybrid model is evaluated by comparing its response to various deformation geometries with analytical model and/or Finite Element Model (FEM). The results show that the hybrid MSS model allows to simulate any compressible isotropic elastic material and in particular the nearly incompressible (Poisson ratio nu approximately equal to 1/2) biological soft tissues to which it is dedicated. |    | 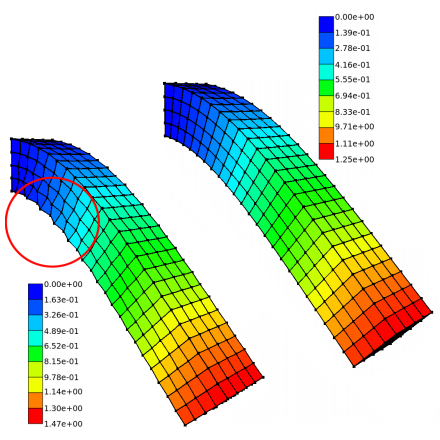 |
| [J23] Approximating Lower-Star Persistence via 2D Combinatorial Map Simplification Damiand G., Paluzo-Hidalgo E., Slechtac R., Gonzalez-Diaz R. Pattern Recognition Letters (PRL), Volume 131, pages 314-321, March 2020 Abstract: Filtration simplification consists of simplifying a given filtration while simultaneously controlling the perturbation in the associated persistence diagrams. In this paper, we propose a filtration simplification algorithm for orientable 2-dimensional (2D) manifolds with or without boundary (meshes) represented by 2D combinatorial maps. Given a lower-star filtration of the mesh, faces are added into contiguous clusters according to a “height” function and a parameter ϵ. Faces in the same cluster are merged into a single face, resulting in a lower resolution mesh and a simpler filtration. We prove that the parameter ϵ bounds the perturbation in the original persistence diagrams, and we provide experiments demonstrating the computational advantages of the simplification process. |    |  |
| [J22] Merge-and-simplify operation for compact combinatorial pyramid definition Damiand G., Zara F. Pattern Recognition Letters (PRL), Volume 129, pages 48-55, January 2020 Abstract: Image pyramids are employed for years in digital image processing. They permit to store and use different scales/levels of details of an image. To represent all the topological information of the different levels, combinatorial pyramids have proved having many interests. But, when using an explicit representation, one drawback of this structure is the memory space required to store such a pyramid. In this paper, this drawback is solved by defining a compact version of combinatorial pyramids. This definition is based on the definition of a new operation, called “merge-and-simplify”, which simultaneously merges regions and simplifies their boundaries. Our experiments show that the memory space of our solution is much smaller than the one of the original version. Moreover, the computation time of our solution is faster, because there are less levels in our pyramid than in the original one. |    | 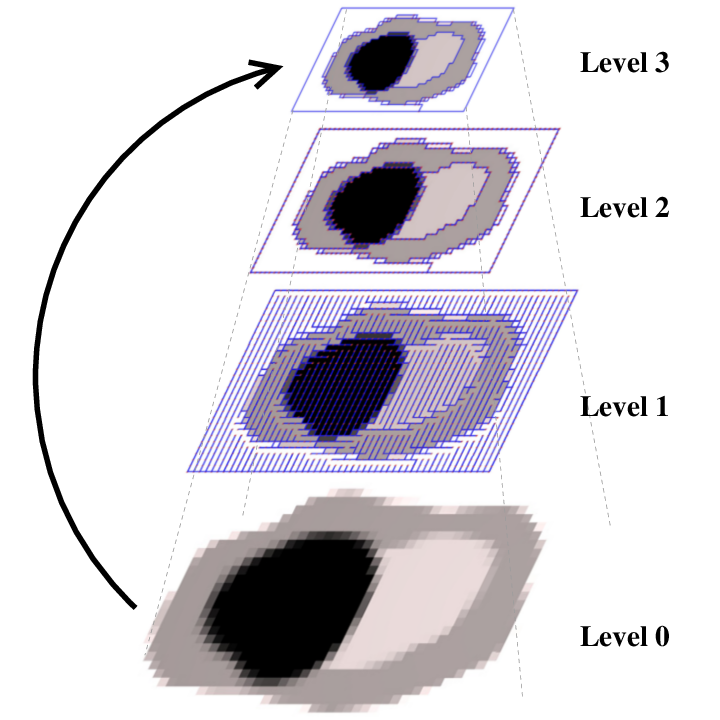 |
| [J21] Distributed Combinatorial Maps for Parallel Mesh Processing Damiand G., Gonzalez-Lorenzo A., Zara F., Dupont F. Algorithms, Volume 11, Number 7, August 2018 Abstract: We propose a new strategy for the parallelization of mesh processing algorithms. Our main contribution is the definition of distributed combinatorial maps (called n-dmaps), which allow us to represent the topology of big meshes by splitting them into independent parts. Our mathematical definition ensures the global consistency of the meshes at their interfaces. Thus, an n-dmap can be used to represent a mesh, to traverse it, or to modify it by using different mesh processing algorithms. Moreover, an nD mesh with a huge number of elements can be considered, which is not possible with a sequential approach and a regular data structure. We illustrate the interest of our solution by presenting a parallel adaptive subdivision method of a 3D hexahedral mesh, implemented in a distributed version. We report space and time performance results that show the interest of our approach for parallel processing of huge meshes. |    | 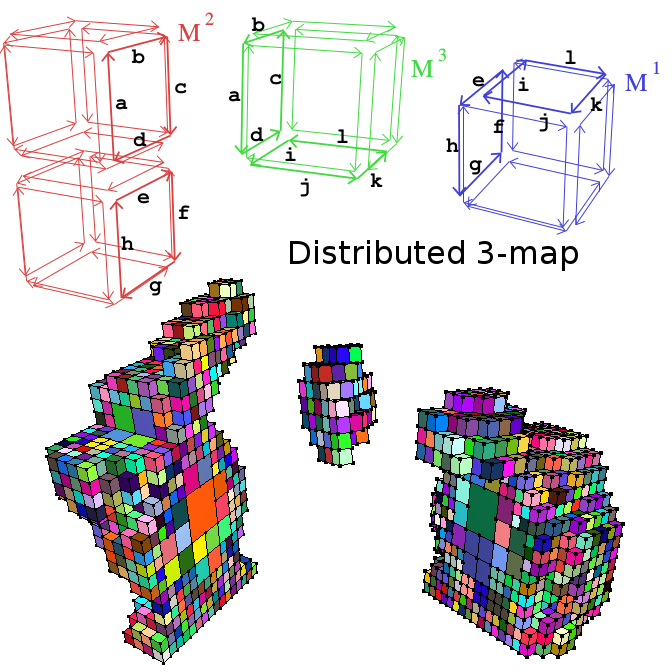 |
| [J20] Hierarchical Representation for Rasterized Planar Face Complexes Damiand G., Gonzalez-Lorenzo A., Rossignac J., Dupont F. Computers & Graphics (C&G), Volume 74, pages 161-170, August 2018 Abstract: A useful example of a Planar Face Complex (PFC) is a connected network of streets, each modeled by a zero-thickness curve. The union of these decomposes the plane into faces that may be topologically complex. The previously proposed rasterized representation of the PFC (abbreviated rPFC) (1) uses a fixed resolution pixel grid, (2) quantizes the geometry of the vertices and edges to pixel-resolution, (3) assumes that no street is contained in a single pixel, and (4) encodes the graph connectivity using a small and fixed number of bits per pixel by decomposing the exact topology into per-pixel descriptors. The hierarchical (irregular) version of the rPFC (abbreviated hPFC) proposed here improved on rPFC in several ways: (1) It uses an adaptively constructed tree to eliminate the “no street in a pixel” constraint of the rPFC, hence making it possible to represent exactly any PFC topology and (2) for PFCs of the models tested, and more generally for models with relatively large empty regions, it reduces the storage cost significantly. |    | 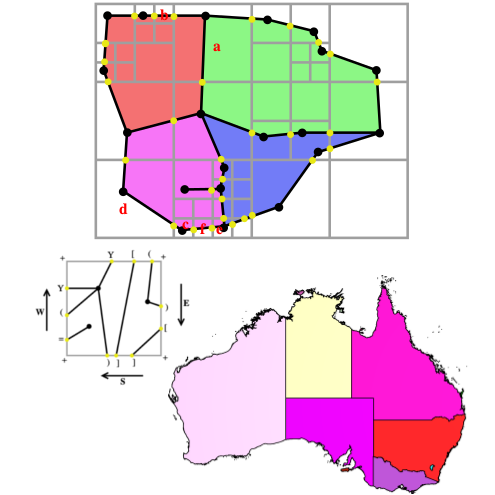 |
| [J19] Rasterized Planar Face Complex Damiand G., Rossignac J. Computer-Aided Design (CAD), Volume 90, pages 146-156, September 2017 Abstract: We consider a Planar Face Complex (PFC). It is defined by the immersion of a planar and connected graph G, which comprises a set of vertices joined by curved edges. G decomposes the plane into faces that need not be manifold or open-regularized and may be bounded by a single loop edge. The PFC may, for example, be used to represent the complex street network of a city, the decomposition of a continent into countries, or the inhomogeneous structure made of a large set of regions of different materials possibly with internal cracks. The rasterized Planar Face Complex (rPFC) proposed here provides a compact representation of an approximation of a PFC, where the precise location of each vertex is quantized to the pixel that contains it and where the precise geometry of each curved edge is approximated by the ordered list (with possible repetitions) of the pixels traversed by (a chosen polygonal approximation of) the edge. We claim three key contributions: (1) The geometric error between a PFC and its rPFC is bounded by the pixel half-diagonal. (2) In spite of such a drastic discretization of the geometry, the rPFC captures the exact topology of the original PFC (provided that no street lies entirely inside a single pixel) and supports standard graph traversal operators that permit to walk the loop of sidewalks along the streets that bound a face, to cross a street to the opposite sidewalk, or to cross streets in order while walking around their common junction. (3) The local connectivity and order information needed to provide the above functionality is stored at each pixel using only about 4 bits per crossing. We discuss the details of this representation, our implementation of its exact construction, four possible embodiments that offer different space/time efficiency compromises, experimental results, relations between rPFC and prior solutions. |    | 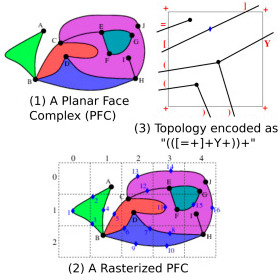 |
| [J18] Homology of Cellular Structures allowing Multi-Incidence Alayrangues S., Damiand G., Lienhardt P., Peltier S. Discrete & Computational Geometry (DCG), Volume 54, Number 1, pages 42-77, July 2015 Abstract: This paper focuses on homology computation over ‘cellular’ structures that allow multi-incidence between cells. We deal here with combinatorial maps, more precisely chains of maps and subclasses such as maps and generalized maps. Homology computation on such structures is usually achieved by computing simplicial homology on a simplicial analog. But such an approach is computationally expensive because it requires computing this simplicial analog and performing the homology computation on a structure containing many more cells (simplices) than the initial one. Our work aims at providing a way to compute homologies directly on a cellular structure. This is done through the computation of incidence numbers. Roughly speaking, if two cells are incident, then their incidence number characterizes how they are attached. Having these numbers naturally leads to the definition of a boundary operator, which induces a homology. Hence, we propose a boundary operator for chains of maps and provide optimization for maps and generalized maps. It is proved that, under specific conditions, the homology of a combinatorial map as defined in the paper is equivalent to the homology of its simplicial analogue. |    |  |
| [J17] On the complexity of Submap Isomorphism and Maximum Common Submap Problems Solnon C., Damiand G., de la Higuera C., Janodet J.-C. Pattern Recognition (PR), Volume 48, Number 2, pages 302-316, February 2015 Abstract: Generalized maps describe the subdivision of objects in cells and are widely used to model 2D and 3D images. In this context, several pattern recognition tasks involve solving submap isomorphism problems (to decide if a map is included in another map) or, more generally, computing maximum common submaps (to measure the distance between two maps). Recently, we have described a polynomial-time algorithm for solving the submap isomorphism problem when the pattern map is connected. In this paper, we show that submap isomorphism is NP-complete when the pattern map is not connected. Then, we characterize the inherent difficulty of submap isomorphism with respect to the number of connected components. We show that it is Fixed-Parameter Tractable (FPT) and we give an FPT algorithm for submap isomorphism. We experimentally compare this algorithm with a state-of-the-art subgraph isomorphism algorithm for searching for patterns in an image and we show that it is both more accurate and more efficient. Finally, we study the complexity of the maximum common submap problem, and we show that it is NP-hard even though we restrict the problem to the search of common connected submaps. |    |  |
| [J16] Polynomial Algorithms for Open Plane Graph and Subgraph Isomorphisms de la Higuera C., Janodet J.-C., Samuel E., Damiand G., Solnon C. Theoretical Computer Science (TCS), Volume 498, pages 76-99, August 2013 Abstract: Graphs are used as models in a variety of situations. In some cases, e.g. to model images or maps, the graphs will be drawn in the plane, and this feature can be used to obtain new algorithmic results. In this work, we introduce a special class of graphs, called open plane graphs, which can be used to represent images or maps for robots: they are planar graphs embedded in the plane, in which certain faces can be removed, are absent or unreachable. We give a normal form for such graphs and prove that one can check in polynomial time if two normalised graphs are isomorphic, or if two open plane graphs are equivalent (their normal forms are isomorphic). Then we consider a new kind of subgraphs, built from subsets of faces and called patterns. We show that searching for a pattern in an open plane graph is tractable if and only if the faces are contiguous, that is, we prove that the problem is NP-complete otherwise. |    |  |
| [J15] From Maximum Common Submaps to Edit Distances of Generalized Maps Combier C., Damiand G., Solnon C. Pattern Recognition Letters (PRL), Volume 33, Number 15, pages 2020-2028, November 2012 Abstract: Generalized maps are widely used to model the topology of nD objects (such as images) by means of incidence and adjacency relationships between cells (vertices, edges, faces, volumes, ...). In this paper, we introduce distance measures for comparing generalized maps, which is an important issue for image processing and analysis. We introduce a first distance measure which is defined by means of the size of a largest common submap. This distance is generic: it is parameterized by a submap relation (which may either be induced or partial), and by weights to balance the importance of darts with respect to seams. We show that this distance measure is a metric. We also introduce a map edit distance, which is defined by means of a minimum cost sequence of edit operations that should be performed to transform a map into another map. We relate maximum common submaps with the map edit distance by introducing special edit cost functions for which they are equivalent. We experimentally evaluate these distance measures and show that they may be used to classify meshes. |    |  |
| [J14] A Generic and Parallel Algorithm for 2D Digital Curve Polygonal Approximation Damiand G., Coeurjolly D. Journal of Real-Time Image Processing (JRTIP), Volume 6, Number 3, pages 145-157, September 2011 Abstract: In this paper, we present a generic topological and geometrical framework which allows to define and control several parallel algorithms for 2D digital curve approximation. The proposed technique is based on combinatorial map simplifications guided by geometrical criteria. We illustrate the genericity of the framework by defining three contour simplification methods: a polygonal approximation one based an area deviation computation; a digital straight segments reconstruction one which guaranties to obtain a loss-less representation; and a moment preserving simplification one which simplifies the contours while preserving geometrical moments of the image regions. Thanks to a complete experimental evaluation, we demonstrate that the proposed methods can be efficiently implemented in a multi-thread environment to simplify labeled image contours. |    |  |
| [J13] Polynomial Algorithms for Subisomorphism of nD Open Combinatorial Maps Damiand G., Solnon C., de la Higuera C., Janodet J.-C., Samuel E. Computer Vision and Image Understanding (CVIU), Volume 115, Number 7, pages 996-1010, July 2011 Abstract: Combinatorial maps describe the subdivision of objects in cells, and incidence and adjacency relations between cells, and they are widely used to model 2D and 3D images. However, there is no algorithm for comparing combinatorial maps, which is an important issue for image processing and analysis. In this paper, we address two basic comparison problems, i.e., map isomorphism, which involves deciding if two maps are equivalent, and submap isomorphism, which involves deciding if a copy of a pattern map may be found in a target map. We formally define these two problems for nD open combinatorial maps, we give polynomial time algorithms for solving them, and we illustrate their interest and feasibility for searching patterns in 2D and 3D images, as any child would aim to do when he searches Wally in Martin Handford's books. |    |  |
| [J12] Fully Deformable 3D Digital Partition Model with Topological Control Damiand G., Dupas A., Lachaud. J.-O. Pattern Recognition Letters (PRL), Volume 32, Number 9, pages 1374-1383, July 2011 Abstract: We propose a purely discrete deformable partition model for segmenting 3D images. Its main ability is to maintain the topology of the partition during the minimization process. To do so, our main contribution is a new definition of multi-label simple points (ML simple point) that is easily computable. An ML simple point can be relabeled without modifying the overall topology of the partition. The definition is based on intervoxel properties, and uses the notion of collapse on cubical complexes. This work is an extension of a former restricted definition [DupasAl09] that prohibits the move of intersections of boundary surfaces. A deformation process is carried out with a greedy energy minimization algorithm. A discrete area estimator is used to approach at best standard regularizers classically used in continuous energy minimizing methods. We illustrate the potential of our approach with the segmentation of 3D medical images with known expected topology. |    | 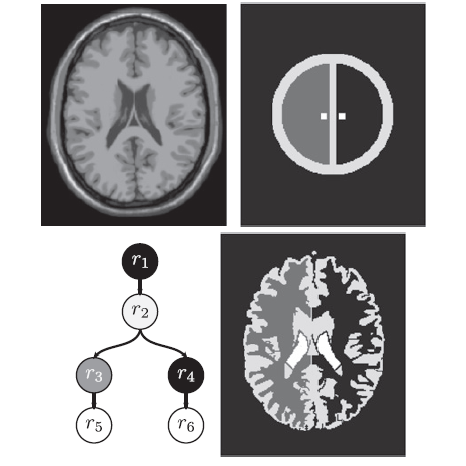 |
| [J11] Efficient Search of Combinatorial Maps using Signatures Gosselin S., Damiand G., Solnon C. Theoretical Computer Science (TCS), Volume 412, Number 15, pages 1392-1405, March 2011 Abstract: In this paper, we address the problem of computing canonical representations of n-dimensional combinatorial maps and of using them for efficiently searching for a map in a database. We define two combinatorial map signatures: the first one has a quadratic space complexity and may be used to decide of isomorphism with a new map in linear time whereas the second one has a linear space complexity and may be used to decide of isomorphism in quadratic time. We show that these signatures can be used to efficiently search for a map in a database. |    | 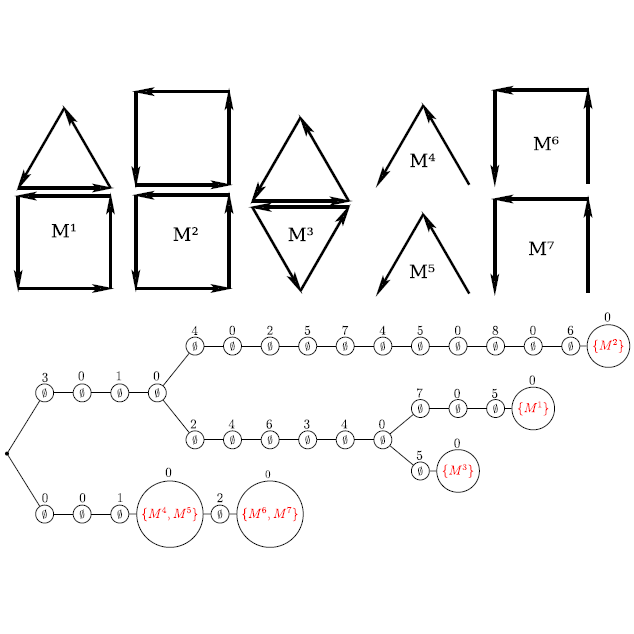 |
| [J10] Tiled top-down combinatorial pyramids for large images representation Goffe R., Brun L., Damiand G. International Journal of Imaging Systems and Technology (IJIST), Volume 21, Number 1, pages 28-36, March 2011 Abstract: The uprising number of applications that involve very large images with resolutions greater than 30000*30000 raises major memory management issues. Firstly, the amount of data usually prevents such images from being processed globally and therefore, designing a global image partition raises several issues. Secondly, a multi-resolution approach is necessary since an analysis only based on the highest resolution may miss global features revealed at lower resolutions. This paper introduces the tiled top-down pyramidal framework which addresses these two main constraints. Our model provides a full representation of multi-resolution images with both geometrical and topological relationships. The advantage of a top-down construction scheme is twofold: the focus of attention only refines regions of interest which results in a reduction of the amount of required memory and in a refinement process that may take into account hierarchical features from previous segmentations. Moreover, the top-down model is combined with a decomposition in tiles to provide an accurate memory bounding while allowing global analysis of large images. |    |  |
| [J9] Region Merging with Topological Control Dupas A., Damiand G. Discrete Applied Mathematics (DAM), Volume 157, Number 16, pages 3435-3446, August 2009 Abstract: This paper presents a region merging process controlled by topological features on regions in 3D images. Betti numbers, a well-known topological invariant, are used as criteria. Classical and incremental algorithms to compute Betti numbers using information represented by the topological map of an image are provided. The region merging algorithm, which allows the merge of any number of connected components of regions together, is explained and its complexity is studied. A topological control of the merging process is implemented using Betti numbers to control the topology of an evolving 3D image partition. The interest of incremental approaches of Betti numbers computation is established by providing processing times comparison. A visual example showing the result of the algorithm and the impact of topological control is also given. |    |  |
| [J8] Directly Computing the Generators of Image Homology using Graph Pyramids Peltier S., Ion A., Kropatsch W.g., Damiand G., Haxhimusa Y. Image and Vision Computing (IMAVIS), Volume 27, Number 7, pages 846-853, June 2009 Abstract: We introduce a method for computing homology groups and their generators of a 2D image, using a hierarchical structure i.e. irregular graph pyramid. Starting from an image, a hierarchy of the image is built, by two operations that preserve homology of each region. Instead of computing homology generators in the base where the number of entities (cells) is large, we first reduce the number of cells by a graph pyramid. Then homology generators are computed efficiently on the top level of the pyramid, since the number of cells is small, and a top down process is then used to deduce homology generators in any level of the pyramid, including the base level i.e. the initial image. The produced generators fit on the object boundaries. A unique set of generators, called the minimal set, is defined and its computation is discussed. We show that the new method produces valid homology generators and present some experimental results. |    |  |
| [J7] Consistency Constraints and 3D Building Reconstruction Horna S., Meneveaux D., Damiand G., Bertrand Y. Computer-Aided Design (CAD), Volume 41, Number 1, pages 13-27, January 2009 Abstract: Virtual architectural (indoor) scenes are often modeled in 3D for various types of simulation systems. For instance, some authors propose methods dedicated to lighting, heat transfer, acoustic or radio-wave propagation simulations. These methods rely in most cases on a volumetric representation of the environment, with adjacency and incidence relationships. Unfortunately, many buildings data are only given by 2D plans and the 3D needs varies from one application to another. To face these problems, we propose a formal representation of consistency constraints dedicated to building interiors and associated with a topological model. We show that such a representation can be used for: (i) reconstructing 3D models from 2D architectural plans (ii) detecting automatically geometrical, topological and semantical inconsistencies (iii) designing automatic and semi-automatic operations to correct and enrich a 2D plan. All our constraints are homogeneously defined in 2D and 3D, implemented with generalized maps and used in modeling operations. We explain how this model can be successfully used for lighting and radio-wave propagation simulations. |    | 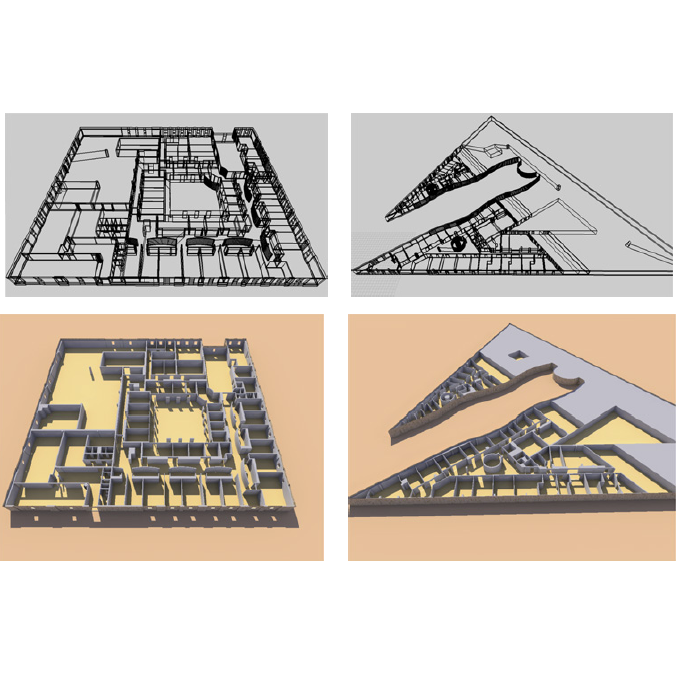 |
| [J6] Topological Model for 3D Image Representation: Definition and Incremental Extraction Algorithm Damiand G. Computer Vision and Image Understanding (CVIU), Volume 109, Number 3, pages 260-289, March 2008 Abstract: In this paper, we define the three-dimensional topological map, a model which represents both the topological and geometrical information of a three-dimensional labeled image. Since this model describes the image's topology in a minimal way, we can use it to define efficient image processing algorithms. The topological map is the last level of map hierarchy. Each level represents the region boundaries of the image and is defined from the previous level in the hierarchy, thus giving a simple constructive definition. This model is an extension of the similar model defined for 2D images. Progressive definition based on successive map levels allows us to extend this model to higher dimension. Moreover, with progressive definition, we can study each level separately. This simplifies the study of disconnection cases and the proofs of topological map properties. Finally, we provide an incremental extraction algorithm which extracts any map of the hierarchy in a single image scan. Moreover, we show that this algorithm is very efficient by giving the results of our experiments made on artificial images. |    | 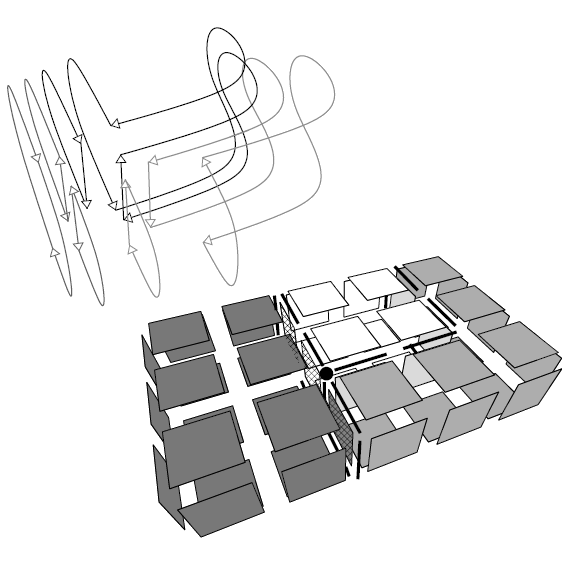 |
| [J5] nD Generalized Map Pyramids: Definition, Representations and Basic Operations Simon C., Damiand G., Lienhardt P. Pattern Recognition (PR), Volume 39, Number 4, pages 527-538, April 2006 Abstract: Graph pyramids are often used for representing irregular image pyramids. For the 2D case, combinatorial pyramids have been recently defined in order to explicitly represent more topological information than graph pyramids. The main contribution of this work is the definition of pyramids of n-dimensional generalized maps. This extends the previous works to any dimension, and generalizes them in order to represent any type of pyramid built by using any removal and/or contraction operations. We give basic algorithms that allow to build an n-dimensional generalized pyramid that describes a multi-level segmented image. A pyramid of n-dimensional generalized maps can be implemented in several ways. We propose three possible representations and give conversion algorithms. |    | 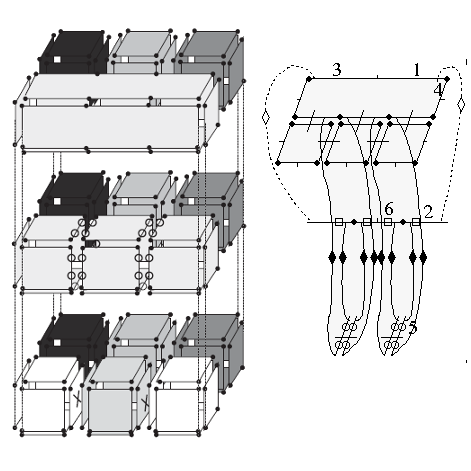 |
| [J4] Removal and Contraction Operations to Define Combinatorial Pyramids: Application to the Design of a Spatial Modeler Damiand G., Dexet-Guiard M., Lienhardt P., Andres E. Image and Vision Computing (IMAVIS), Volume 23, Number 2, pages 259-269, February 2005 Abstract: Removal and contraction are basic operations for several methods conceived in order to handle irregular image pyramids, for multi-level image analysis for instance. We give the definitions of removal and contraction operations in the generalized maps framework. We propose a first experimentation of irregular pyramid as a basis for a discrete geometrical modeler that can handle both discrete and continuous representations of geometrical objects. This modeler is based on a pyramidal kernel with four coexisting levels between the discrete and the Euclidean representations. We describe how this pyramid can be constructed and updated. |    | 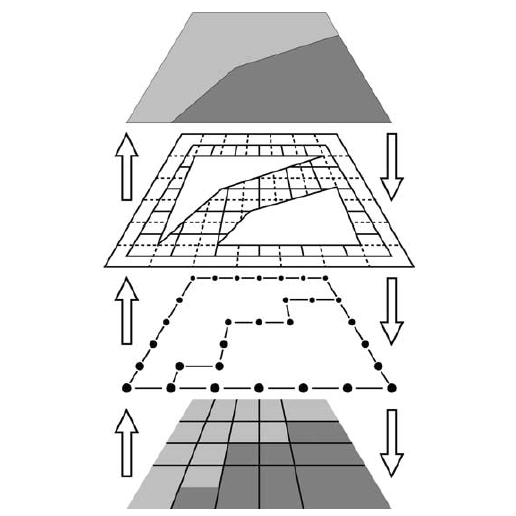 |
| [J3] Topological Model for Two-Dimensional Image Representation: Definition and Optimal Extraction Algorithm Damiand G., Bertrand Y., Fiorio C. Computer Vision and Image Understanding (CVIU), Volume 93, Number 2, pages 111-154, February 2004 Abstract: In this paper, we define the two-dimensional topological map, a model which represents both topological and geometrical information of a two-dimensional labeled image. Since this model is minimal, complete, and unique, we can use it to define efficient image processing algorithms. The topological map is the last level of a map hierarchy. Each level represents the region boundaries of the image and is defined from the previous one in the hierarchy, thus giving a simple constructive definition. This model is similar to two existing structures but the main innovation of our approach is the progressive definition based on the successive map levels. These different maps can easily be extended in order to define the topological map in any dimension. Furthermore we provide an optimal extraction algorithm which extracts the different maps of the hierarchy in a single image scan. This algorithm is based on local configurations called precodes. Due to our constructive definition, different configurations are factorized which simplifies the implementation. |    |  |
| [J2] Split and Merge Algorithms Defined on Topological Maps for 3D Image Segmentation Damiand G., Resch P. Graphical Models (GM), Volume 65, Number 1-3, pages 149-167, May 2003 Abstract: Split-and-merge algorithms define a class of image segmentation methods. Topological maps are a mathematical model that represents image subdivisions in 2D and 3D. This paper discusses a split-and-merge method for 3D image data based on the topological map model. This model allows representations of states of segmentations and of merge and split operations. Indeed, it can be used as data structure for dynamic changes of segmentation. The paper details such an algorithmic approach and analyzes its time complexity. A general introduction into combinatorial and topological maps is given to support the understanding of the proposed algorithms. |    |  |
| [J1] A Simple Paradigm for Graph Recognition: Application to Cographs and Distance Hereditary Graphs Damiand G., Habib M., Paul C. Theoretical Computer Science (TCS), Volume 263, Number 1-2, pages 99-111, July 2001 Abstract: An easy way for graphs recognition algorithms is to use a two-steps process. First compute a characteristic feature as if the graph belong to that class. Secondly check whether the computed feature really defines the input graphs. Although in some cases the two steps can be merged. But separating them may yield to new and much more easily understood algorithms. In this paper we apply that paradigm to the cographs and distance hereditary graphs recognition problem. |    |  |
| International Conferences |
| [C56] Persistent Homology Computation Using Combinatorial Map Simplification Damiand G., Gonzalez-Diaz R. Proc. of 7th International Workshop on Computational Topology in Image Context (CTIC), Lecture Notes in Computer Science 11382, pages 26-39, January 2019, Malaga, Spain Abstract: We propose an algorithm for persistence homology computation of orientable 2-dimensional (2D) manifolds with or without boundary (meshes) represented by 2D combinatorial maps. Having as an input a real function h on the vertices of the mesh, we first compute persistent homology of filtrations obtained by adding cells incident to each vertex of the mesh, The cells to add are controlled by both the function h and a parameter delta. The parameter delta is used to control the number of cells added to each level of the filtration. Bigger delta produces less levels in the filtration and consequently more cells in each level. We then simplify each level (cluster) by merging faces of the same cluster. Our experiments demonstrate that our method allows fast computation of persistent homology of big meshes and it is persistent-homology aware in the sense that persistent homology does not change in the simplification process when fixing delta. |    |  |
| [C55] An automatic comparison approach to detect errors on 3D city models Gorszczyk B., Damiand G., Servigne S., Diakité A. A., Gesquière G. Proc. of 4th Eurographics Workshop on Urban Data Modelling and Visualisation (UDMV), pages 25-30, July 2016, Liège, Belgium Abstract: 3D building models are needed in several professional domains. To provide better results, these models must be errors-free and that is why it is required to have a way to detect and to correct errors. These errors can be geometric, topological or semantic. By using a topological structure called EBM-LCC that allows to model buildings, we create a new tool that allows to detect these three type of errors in 3D city models. The solution we propose is an algorithm that compares two EBM-LCC. This algorithm can be used to compare two different models, for example acquired with two different processes, or resulting from two different acquisition campaigns. It is also an interesting tool to compare and validate algorithms. In this work, we compare an EBM-LCC loaded directly from a CityGML model with an EBM-LCC reconstructed from a soup of polygons only. Then we can use the result of this comparison to outline possible differences or to correct one of the two models by using the information of the other one. This algorithm allowed to automatically detect and correct semantic errors on several models that are currently used by professionals. This shows the interest of EBM-LCC for the city modeling domain as it helps to reach an error-free model. |    |  |
| [C54] New Mass Spring System formulation to model the behavior of soft tissues Golec K., Zara F., Nicolle S., Palierne J.-F., Damiand G. Proc. of 22nd European Society of Biomechanics Congress (ESB), July 2016, Lyon, France Abstract: Computer-based medicine has been largely developed in recent years for helping surgery, diagnosis and treatment. Unfortunately, from a mechanical standpoint, modeling complex materials such as soft tissues is still a challenge requiring accuracy and possibility of user interaction. Among computational models (such as Finite Element Method, or Position Based Dynamics), we chose the Mass-Spring System (MSS) as model. It offers several advantages, like adaptability and fast computation, while allowing topological modifications (like cutting or piercing) without pre-computations. In this paper we present a new MSS formulation for soft tissue simulations. The validation of the mechanical response of the model is based on work of Nicolle et al. which reported the shear behavior of three vital internal organs (kidney, liver and spleen). Our method is based on a topological-physical model called TopoSim which allows to easily implement different physical models and performs fast and accurate modeling of different kinds of tissues. Thanks to this model, we are able to easily adapt the simulation to desired requirements and to perform topological modifications during simulations if necessary. |    | 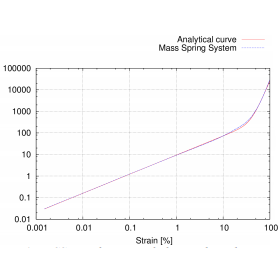 |
| [C53] Parallel Homology Computation of Meshes Damiand G., Gonzalez-Diaz R. Proc. of 6th International Workshop on Computational Topology in Image Context (CTIC), Lecture Notes in Computer Science 9667, pages 53-64, June 2016, Marseille, France Abstract: In this paper, we propose a method to compute, in parallel, the homology groups of closed meshes (i.e., orientable 2D manifolds without boundary) represented by combinatorial maps. Our experiments illustrate the interest of our approach which is really fast on big meshes and which obtains good speed-up when increasing the number of threads. |    |  |
| [C52] Combining Geometry, Topology and Semantics for Generic Building Description and Simulations Horna S., Damiand G., Diakité A. A., Meneveaux D. Proc. of 3rd Eurographics Workshop on Urban Data Modelling and Visualisation (UDMV), Eurographics Digital Library, pages 13-18, November 2015, Delft, the Netherlands Abstract: 2D and 3D virtual architectural models are the common ground of many studies, including environmental protection, energy saving, or human well-being. Building or urban environment simulations concern for instance heat transfer, lighting, and acoustics, each of them requiring physical parameters additionally to the geometric representation. Furthermore, geometry does not generally comply straightforwardly with physical parameters and users are forced to manually adapt the models before simulation. This paper proposes an overview of modeling and simulation studies that make use of topological representations, and discusses the advantages of a topological representation for various types of applications. Such a representation can be used not only to maintain the 3D model global coherence, but also to automatically retrieve walls, doors, or room volumes for instance. Based on the existing model of generalized maps, this paper also illustrates some examples of structure traversal that can be used for providing the users with adequate simulation data. |    |  |
| [C51] Incremental Updating of 3D Topological Maps to Describe Videos Damiand G., Brandel S., Conte D. Proc. of 17th International Workshop on Combinatorial Image Analysis (IWCIA), Lecture Notes in Computer Science 9448, pages 299-310, November 2015, Kolkata, India Abstract: A topological map is an efficient mathematical model for representing an image subdivision where all cells and adjacency relations between elements are represented. It has been proved to be a very good tool for video processing when video is seen as a 3D image. However the construction of a topological map for representing a video needs the availability of the complete image sequence. In this paper we propose a procedure for online updating a topological map in order to build it as the video is produced, allowing to use it in real time. |    |  |
| [C50] Improvement of a Topological-Physical Model to manage different physical simulations Golec K., Coquet M., Zara F., Damiand G. Proc. of 23rd International Conference in Central Europe on Computer Graphics, Visualization and Computer Vision (WSCG), WSCG Full papers proceedings, pages 25-34, June 2015, Plzen, Czech Republic Abstract: We present an improvement of a unified topological-physical model which permits topological modifications during physical simulation of soft tissues. Our improvement makes the model more generic, efficient and simpler to update. The main principle of our improvement is to associate information to elements of the model, depending on the underlying physical model. Our modification of the architecture enables to easily integrate different physical models. Moreover, topological operations and physical simulations can be factorized between the different physical models. Our solution is more efficient as it leads to simpler modification algorithms after topological alterations with less changes to apply. In this paper, we present our new solution and illustrate its new properties thanks to several experiments performed on two well-known physical models: Mass-Spring System and Tensor-Mass model. The results present a comparison of our solution with the previous one for the cutting topological operation. Moreover, as our model permits to easily compare several physical models, we performed some simulations to reproduce experiments made on real tissues. |   |  |
| [C49] Automatic Semantic Labelling of 3D Buildings Based on Geometric and Topological Information Diakité A. A., Damiand G., Gesquière G. Proc. of 9th International 3DGeoInfo Conference (3DGeoInfo), 3DGeoInfo conference proceedings series, pages 49-63, November 2014, Dubai, United Arab Emirates Abstract: The lack of suitable information in 3D models of buildings and cities is still a strong limitation for the increasing number of applications requiring the 3D data. The latter are often obtained from acquisition or modeling processes during which the geometry is well preserved, but the topological and semantic information are lost. We present a new approach to enrich a purely geometric model with topological information. The reconstructed topology combined to the geometry is helpful to several operations like guided building simplification, model correction, etc. In this work we recover the semantic information based on a propagation approach guided by heuristic rules. All the process is automatic and designed such that any user can bring and customize as many rules as needed to supervise the semantic labelling. As example we propose few rules applied to both Building Information Models (BIM) and 3D Geometric Information Systems (GIS) data. |    |  |
| [C48] A Generic Implementation of dD Combinatorial Maps in CGAL Damiand G., Teillaud M. Proc. of 23rd International Meshing Roundtable (IMR), Procedia Engineering 82, pages 46-58, October 2014, London, United Kingdom Abstract: We present a generic implementation of dD combinatorial maps and linear cell complexes in Cgal, the Computational Geometry Algorithms Library. A combinatorial map describes an object subdivided into cells; a linear cell complex describes the linear geometry embedding of such a subdivision. In this paper, we show how generic programming and new techniques recently introduced in the C++11 standard allow a fully generic and customizable implementation of these two data structures, while maintaining optimal memory footprint and direct access to all information. We compare our implementation with existing 2D and 3D libraries implementing cellular structures, and illustrate its usage by two applications. To the best of our knowledge, the Cgal software package presented here offers the only available generic implementation of combinatorial maps in any dimension. |    |  |
| [C47] A Unified Topological-Physical Model for Adaptive Refinement Fléchon E., Zara F., Damiand G., Jaillet F. Proc. of 11th Workshop on Virtual Reality Interaction and Physical Simulation (VRIPHYS), Eurographics Digital Library, pages 39-48, September 2014, Bremen, Germany Abstract: In Computer Graphics, physically-based simulation of deformable objects is a current challenge, and many efficient models have been developed to reach real-time performance. However, these models are often limited when complex interactions involving topological modifications are required. To overcome this, the key issue is to manage concurrently, and at minimal cost, both the topology and physical properties. Thus, this paper presents a unified topological-physical model for soft body simulation. The complete embedding of physical and topological models will facilitate operations like piercing, fracture or cutting, as well as adaptive refinement. Indeed, the difficulty is to treat topological changes during the simulation, requiring combined geometric and physics considerations. Rigorous topological operations guarantee the validity of the mesh, while direct access to the adjacent and incident relations will ease the update of physical properties of new elements created during these operations. These features are illustrated on an embedded mass-spring system undergoing topological modifications performed during simulation. Different levels of subdivision are also presented. |    |  |
| [C46] 2D Topological Map Isomorphism for Multi-label Simple Transformation Definition Damiand G., Roussillon T., Solnon C. Proc. of 18th International Conference on Discrete Geometry for Computer Imagery (DGCI), Lecture Notes in Computer Science 8668, pages 39-50, September 2014, Siena, Italy Abstract: A 2D topological map allows one to fully describe the topology of a labeled image. In this paper we define 2D topological map isomorphism. We show that isomorphic topological maps correspond to homeomorphic embeddings in the plane and we give a polynomial-time algorithm for deciding of topological map isomorphism. Then we use this notion to give a generic definition of multi-label simple transformation as a set of transformations of labels of pixels which does not modify the topology of the labeled image. We illustrate the interest of multi-label simple transformation by generating look-up tables of any pair of adjacent pixel transformation preserving the topology. |    |  |
| [C45] Remove Noise in Video with 3D Topological Maps Conte D., Damiand G. Proc. of 15th International Workshop on Structural and Syntactic Pattern Recognition (SSPR), Lecture Notes in Computer Science 8621, pages 213-222, August 2014, Joensuu, Finland Abstract: In this paper we present a new method for foreground masks denoising in videos. Our main idea is to consider videos as 3D images and to deal with regions in these images. Denoising is thus simply achieved by merging foreground regions corresponding to noise with background regions. In this framework, the main question is the definition of a criterion allowing to decide if a region corresponds to noise or not. Thanks to our complete cellular description of 3D images, we can propose an advanced criterion based on Betti numbers, a topological invariant. Our results show the interest of our approach which gives better results than previous methods. |    |  |
| [C44] Topological Reconstruction of Complex 3D Buildings and Automatic Extraction of Levels of Detail Diakité A. A., Damiand G., Van Maercke D. Proc. of 2nd Eurographics Workshop on Urban Data Modelling and Visualisation (UDMV), Eurographics Digital Library, pages 25-30, April 2014, Strasbourg, France Abstract: This paper describes a new method allowing to retrieve the indoor and outdoor topology of a detailed 3D building model from its geometry and to extract different levels of detail (LoD) from the ersulting topological description. No prior information about the initial model, except its geometric information is needed as input, and using the combinatorial maps data structure, the method recovers the topological information of the identified parts of the building. The topology is needed for most of the applications using 3D building models after the architects design it. While classical models available are mainly furnished in a Boundary Representation (B-Rep) format, we discuss how to recover the components that allow to distinguish the several parts of the building (defined as volumes) then the spatial relationships linking them. |    |  |
| [C43] Constructing an n-dimensional cell complex from a soup of (n-1)-dimensional faces Arroyo Ohori K., Damiand G., Ledoux H. Proc. of 1st International Conference on Applied Algorithms (ICAA), Lecture Notes in Computer Science 8321, pages 37-48, January 2014, Kolkata, India Abstract: There is substantial value in the use of higher-dimensional (>3D) digital objects in GIS that are built from complex real-world data. This use is however hampered by the difficulty of constructing such objects. In this paper, we present a dimension independent algorithm to build an n-dimensional cellular complex with linear geometries from its isolated (n-1)-dimensional faces represented as combinatorial maps. It does so by efficiently finding the common (n-2)-cells (ridges) along which they need to be linked. This process can then be iteratively applied in increasing dimension to construct objects of any dimension. We briefly describe combinatorial maps, present our algorithm using them as a base, and show an example using 2D, 3D and 4D objects which was verified to be correct, both manually and using automated methods. |    |  |
| [C42] A generic topological framework for physical simulation Fléchon E., Zara F., Damiand G., Jaillet F. Proc. of 21th International Conference in Central Europe on Computer Graphics, Visualization and Computer Vision (WSCG), WSCG Full papers proceedings, pages 104-113, June 2013, Plzen, Czech Republic Abstract: This paper presents the use of a topological model to simulate a soft body deformation based on a Mass-Spring System. We provide a generic framework which can integrate any kind of geometrical meshes (hexahedral or tetrahedral elements), using several numerical integration schemes (Euler semi-implicit or implicit). This framework naturally allows topological changes in the simulated object during the animation. Our model is based on the 3D Linear Cell Complex topological model (itself based on a 3D combinatorial map), adding the extra information required for simulation purposes. Moreover, we present some adaptations performed on this data structure to fit our simulation requirements, and to allow efficient cutting or piercing in a 3D object. |   |  |
| [C41] Map Edit Distance vs Graph Edit Distance for Matching Images Combier C., Damiand G., Solnon C. Proc. of 9th Workshop on Graph-Based Representation in Pattern Recognition (GBR), Lecture Notes in Computer Science 7877, pages 152-161, May 2013, Vienna, Austria Abstract: Generalized maps are widely used to model the topology of nD objects (such as 2D or 3D images) by means of incidence and adjacency relationships between cells (0D vertices, 1D edges, 2D faces, 3D volumes, ...). Recently, we have introduced a map edit distance. This distance compares maps by means of a minimum cost sequence of edit operations that should be performed to transform a map into another map. In this paper, we introduce labelled maps and we show how the map edit distance may be extended to compare labeled maps. We experimentally compare our map edit distance to the graph edit distance for matching regions of different segmentations of a same image. |    |  |
| [C40] On the complexity of Submap Isomorphism Solnon C., Damiand G., De La Higuera C., Janodet J.-C. Proc. of 9th Workshop on Graph-Based Representation in Pattern Recognition (GBR), Lecture Notes in Computer Science 7877, pages 21-30, May 2013, Vienna, Austria Abstract: Generalized maps describe the subdivision of objects in cells, and incidence and adjacency relations between cells, and they are widely used to model 2D and 3D images. Recently, we have defined submap isomorphism, which involves deciding if a copy of a pattern map may be found in a target map, and we have described a polynomial time algorithm for solving this problem when the pattern map is connected. In this paper, we show that submap isomorphism becomes NP-complete when the pattern map is not connected, by reducing the NP-complete problem Planar-4 3-SAT to it. |    | 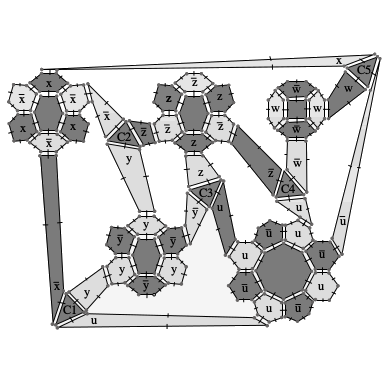 |
| [C39] Removal Operations in nD Generalized Maps for Efficient Homology Computation Damiand G., Gonzalez-Diaz R., Peltier S. Proc. of 4th International Workshop on Computational Topology in Image Context (CTIC), Lecture Notes in Computer Science 7309, pages 20-29, May 2012, Bertinoro, Italy Abstract: In this paper, we present an efficient way for computing homology generators of nD generalized maps. The algorithm proceeds in two steps: (1) cell removals reduces the number of cells while preserving homology; (2) homology generator computation is performed on the reduced object by reducing incidence matrices into their Smith-Agoston normal form. In this paper, we provide a definition of
cells that can be removed while preserving homology. Some results on 2D and 3D homology generators computation are presented. |    |
| [C38] Frequent Submap Discovery Gosselin S., Damiand G., Solnon C. Proc. of 22nd Symposium on Combinatorial Pattern Matching (CPM), Lecture Notes in Computer Science 6661, pages 429-440, June 2011, Palermo, Italy Abstract: Combinatorial maps are nice data structures for modeling the topology of nD objects subdivided in cells (e.g., vertices, edges, faces, volumes, ...) by means of incidence and adjacency relationships between these cells. In particular, they can be used to model the topology of plane graphs. In this paper, we describe an algorithm, called mSpan, for extracting patterns which occur frequently in a database of maps. We experimentally compare mSpan with gSpan on a synthetic database of randomly generated 2D and 3D maps. We show that gSpan does not extract the same patterns, as it only considers adjacency relationships between cells. We also show that mSpan exhibits nicer scale-up properties when increasing map sizes or when decreasing frequency. |    | 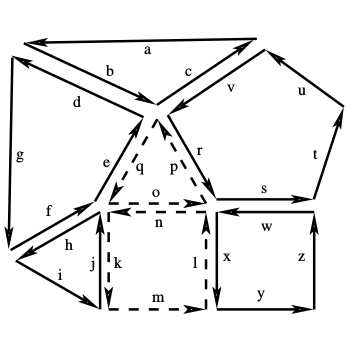 |
| [C37] Combining Topological Maps, Multi-Label Simple Points, and Minimum-Length Polygons for Efficient Digital Partition Model Damiand G., Dupas A., Lachaud J.-O. Proc. of 14th International Workshop on Combinatorial Image Analysis (IWCIA), Lecture Notes in Computer Science 6636, pages 56-69, May 2011, Madrid, Spain Abstract: Deformable models have shown great potential for image segmentation. They include discrete models whose combinatorial formulation leads to efficient and sometimes optimal minimization algorithms. In this paper, we propose a new discrete framework to deform any partition while preserving its topology. We show how to
combine the use of multi-label simple points, topological maps and minimum-length polygons in order to implement an efficient digital deformable partition model. Our experimental results illustrate the
potential of our framework for segmenting images, since it allows the mixing of region-based, contour-based and regularization energies, while keeping the overall image structure. |    | 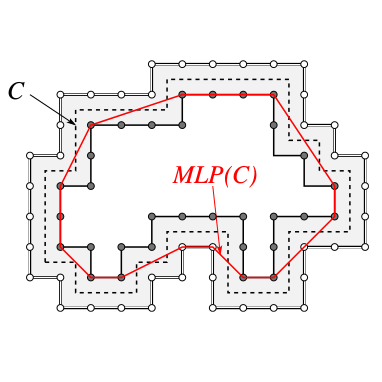 |
| [C36] Measuring the Distance of Generalized Maps Combier C., Damiand G., Solnon C. Proc. of 8th Workshop on Graph-Based Representation in Pattern Recognition (GBR), Lecture Notes in Computer Science 6658, pages 82-91, May 2011, Münster, Germany Abstract: Generalized maps are widely used to model the topology of nD objects (such as images) by means of incidence and adjacency relationships between cells (vertices, edges, faces, volumes, ...). In this paper, we define a first error-tolerant distance measure for comparing generalized maps, which is an important issue for image processing and analysis. This distance measure is defined by means of the size of a largest common submap, in a similar way as a graph distance measure may be defined by means of the size of a largest common subgraph. We show that this distance measure is a metric, and we introduce a greedy randomized algorithm which allows us to efficiently compute an upper bound of it. |    |  |
| [C35] Tiled Top-Down Pyramids and Segmentation of Large Histological Images Goffe R., Brun L., Damiand G. Proc. of 8th Workshop on Graph-Based Representation in Pattern Recognition (GBR), Lecture Notes in Computer Science 6658, pages 255-264, May 2011, Münster, Germany Abstract: Recent microscopic imaging systems such as whole slide scanners provide very large (up to 18GB) high resolution images. Such amounts of memory raise major issues that prevent usual image representation models from being used. Moreover, using such high resolution images, global image features, such as tissues, does not clearly appear at full resolution. Such images contain thus different hierarchical information at different resolutions. This paper presents the model of tiled top-down pyramids which provides a framework to handle such images. This model encodes a hierarchy of partitions of large images defined at different resolutions. We also propose a generic construction scheme of such pyramids whose validity is evaluated on an histological image application. |    |  |
| [C34] A Causal Extraction Scheme in Top-Down Pyramids for Large Images Segmentation Goffe R., Damiand G., Brun L. Proc. of 13th International Workshop on Structural and Syntactic Pattern Recognition (SSPR), Lecture Notes in Computer Science 6218, pages 264-274, August 2010, Cesme, Izmir, Turkey Abstract: Applicative fields based on the analysis of large images must deal with two important problems. First, the size in memory of such images usually forbids a global image analysis hereby inducing numerous problems for the design of a global image partition. Second, due to the high resolution of such images, global features only appear at low resolutions and a single resolution analysis may loose important information. The tiled top-down pyramidal model has been designed to solve this two major challenges. This model provides a hierarchical encoding of the image at single or multiple resolutions using a top-down construction scheme. Moreover, the use of tiles bounds the amount of memory required by the model while allowing global image analysis. The main limitation of this model is the splitting step used to build one additional partition from the above level. Indeed, this step requires to temporary refine the split region up to the pixel level which entails high memory requirements and processing time. In this paper, we propose a new splitting step within the tiled top-down pyramidal framework which overcomes the previously mentioned limitations. |    |  |
| [C33] Signatures of Combinatorial Maps Gosselin S., Damiand G., Solnon C. Proc. of 13th International Workshop on Combinatorial Image Analysis (IWCIA), Lecture Notes in Computer Science 5852, pages 370-382, November 2009, Cancun, Mexico Abstract: In this paper, we address the problem of computing a canonical representation of an n-dimensional combinatorial map. For that, we define two combinatorial map signatures: the first one has a quadratic space complexity and may be used to decide of isomorphism with a new map in linear time whereas the second one has a linear space complexity and may be used to decide of isomorphism in quadratic time. Experimental results show that these signatures can be used to recognize images very efficiently. |    |  |
| [C32] Extraction of tiled top-down irregular pyramids from large images Goffe R., Damiand G., Brun L. Proc. of 13th International Workshop on Combinatorial Image Analysis (IWCIA), Research Publishing Services, pages 123-137, November 2009, Cancun, Mexico Abstract: Processing large images is a common issue in the computer vision framework with applications such as satellite or microscopic images. The major problem comes from the size of those images that prevents them from being loaded globally into memory. Moreover, such images contain different information at different levels of resolution. For example, global features, such as the delimitation of a tissue, appear at low resolution whereas finer details, such as cells, can only be distinguished at full resolution. Thus, the objective of this paper is the definition of a suitable hierarchical data structure that would provide full access to all the properties of the image by representing topological information. The idea consists in transposing the notion of tile for top-down topological pyramids to control accurately the amount of memory required by the construction of our model. As a result, this paper defines the topological model of tiled top-down pyramid and proposes a construction scheme that would not depend on the system memory limitations. |   |  |
| [C31] Multi-Label Simple Points Definition for 3D Images Digital Deformable Model Dupas A., Damiand G., Lachaud J.-O. Proc. of 15th International Conference on Discrete Geometry for Computer Imagery (DGCI), Lecture Notes in Computer Science 5810, pages 156-167, September 2009, Montréal, Canada Abstract: We present a new deformable partition model, with a natural application to image segmentation. Our approach is purely digital: the partition geometry is the set of intervoxel elements that are between regions and is thus a set of digital surfaces. We define the new notion of I-Simple points to ensure that the partition topology remains unchanged during deformations. This definition is based on simple intervoxel properties and is easy to implement. The deformation is carried out with a greedy energy minimization algorithm. A discrete area estimator is used to approach at best standard regularizers classically used in continuous energy minimizing methods. The effectiveness of our approach is shown on several 3D image segmentations. |    |  |
| [C30] Border Operator for Generalized Maps Alayrangues S., Peltier S., Damiand G., Lienhardt P. Proc. of 15th International Conference on Discrete Geometry for Computer Imagery (DGCI), Lecture Notes in Computer Science 5810, pages 300-312, September 2009, Montréal, Canada Abstract: In this paper, we define a border operator for the generalized maps, a data structure for representing cellular quasi-manifolds. The interest of this work lies in the optimization of homology computation, by using a model with less cells than models in which cells are regular ones as tetrahedra and cubes. For instance, generalized maps have been used for representing segmented images. We first define a face operator to retrieve the faces of any cell, then deduce the border operator and prove that it satisfies the required property : border of border is void. At last, we study the links between the cellular homology defined from our border operator and the classical simplicial homology. |    |  |
| [C29] Homology Computation on Cellular Structures in Image Context Alayrangues S., Damiand G., Fuchs L., Lienhardt P., Peltier S. Proc. of 2nd International Workshop on Computational Topology in Image Context (CTIC), pages 19-28, August 2009, St. Kathrein/Offenegg, Austria Abstract: During the previous decade, many works have shown that topological properties are of interest in an image context. Among all topological invariants (Euler characteristic, Betti numbers, orientability...), homology groups are known to be powerful (in term of topological characterization) and computable in the same way in any dimension. In this paper, we recall briefly the cellular structures used in topology-based geometric modeling and image analysis, and propose different approaches for computing homology on such structures. These approaches are adaptations of classical methods from algebraic topology that had essentially been developed for simplicial or cubical complexes. We present two works in progress dealing with two different methods for computing homology information on structures derived from combinatorial maps: a method relying on the definition of a cellular border operator, the other following a constructive approach based on the works about effective homology. |   |  |
| [C28] A Polynomial Algorithm for Subisomorphism of Holey Plane Graphs Damiand G., De La Higuera C., Janodet J.-C., Samuel E., Solnon C. Proc. of 7th International Workshop on Mining and Learning with Graphs (MLG), July 2009, Leuven, Belgium Abstract: We address the problem of searching for a pattern in a plane graph, that is, a planar drawing of a planar graph. We define plane subgraph isomorphism and give a polynomial algorithm for this problem. We show that this algorithm may be used even when the pattern graph has holes. |    |  |
| [C27] Polynomial Algorithm for Submap Isomorphism: Application to Searching Patterns in Images Damiand G., De La Higuera C., Janodet J.-C., Samuel E., Solnon C. Proc. of 7th Workshop on Graph-Based Representation in Pattern Recognition (GBR), Lecture Notes in Computer Science 5534, pages 102-112, May 2009, Venice, Italy Abstract: In this paper, we address the problem of searching for a pattern in a plane graph, i.e., a planar drawing of a planar graph. To do that, we propose to model plane graphs with 2-dimensional combinatorial maps, which provide nice data structures for modelling the topology of a subdivision of a plane into nodes, edges and faces. We define submap isomorphism, we give a polynomial algorithm for this problem, and we show how this problem may be used to search for a pattern in a plane graph. First experimental results show the validity of this approach to efficiently search for patterns in images. |    |  |
| [C26] 3D Topological Map Extraction from Oriented Boundary Graph Baldacci F., Braquelaire A., Damiand G. Proc. of 7th Workshop on Graph-Based Representations in Pattern Recognition (GBR), Lecture Notes in Computer Science 5534, pages 283-292, May 2009, Venice, Italy Abstract: The extraction of a 3D topological map from an Oriented Boundary Graph can be needed to refine a 3D Split and Merge segmentation using topological information such as the Euler characteristic of regions. A presegmentation could thus be efficiently obtained using a light structuring model, before proceeding to the extraction of more information on some regions of interest. In this paper, we present the topological map extraction algorithm which allows to reconstruct locally a set of regions from the Oriented Boundary Graph. A comparison of the two models is also presented. |    | 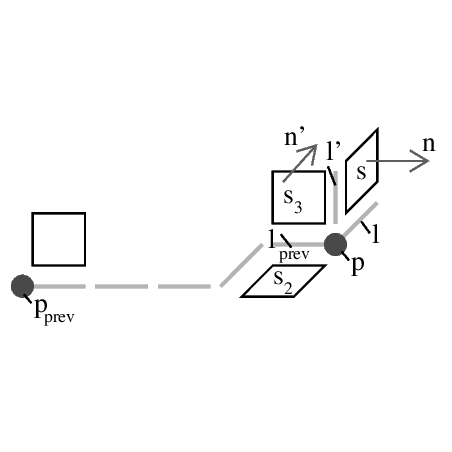 |
| [C25] A Top-Down Construction Scheme for Irregular Pyramids Goffe R., Brun L., Damiand G. Proc. of 4th International Conference On Computer Vision Theory And Applications (VISAPP), pages 163-170, February 2009, Lisboa, Portugal Abstract: Hierarchical data structures such as irregular pyramids are used by many applications related to image processing and segmentation. The construction scheme of such pyramids is bottom-up. Such a scheme forbids the definition of a level according to more global information defined at upper levels in the hierarchy. Moreover, the base of the pyramid has to encode any single pixel of the initial image in order to allow the definition of regions of any shape at higher levels. This last constraint raises major issues of memory usage and processing costs when irregular pyramids are applied to large images. The objective of this paper is to define a top-down construction scheme for irregular pyramids. Each level of such a pyramid is encoded by a combinatorial map associated to an explicit encoding of the geometry and the inclusion relationships of the corresponding partition. The resulting structure is a stack of finer and finer partitions obtained by successive splitting operations and is called a top-down pyramid. |    | 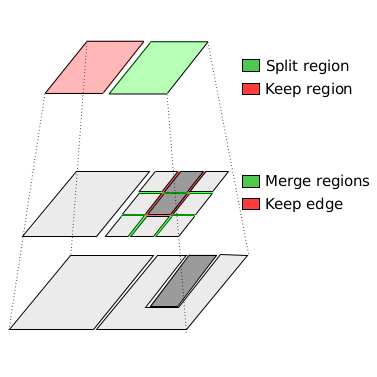 |
| [C24] A Generic and Parallel Algorithm for 2D Image Discrete Contour Reconstruction Damiand G., Coeurjolly D. Proc. of 4th International Symposium on Visual Computing (ISVC), Lecture Notes in Computer Science 5359, pages 792-801, December 2008, Las vegas, Nevada, USA Abstract: In this paper, we present a generic topological and geometrical framework for the digital reconstruction of complex contours from labeled images. The proposed technique is based on combinatorial map simplifications guided by digital straight segments. We illustrate the genericity of the framework with a parallel contour reconstruction algorithm. |    | 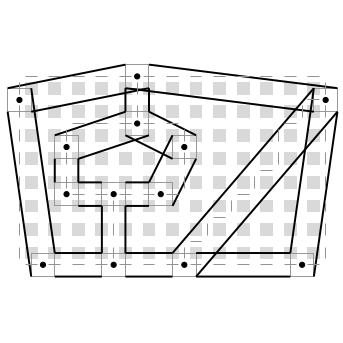 |
| [C23] Computing Canonical Polygonal Schemata with Generalized Maps Damiand G., Alayrangues S. Proc. of International Conference on Topological & Geometric Graph Theory (TGGT), Electronic Notes in Discrete Mathematics 31, pages 287-292, August 2008, Paris, France Abstract: The comparison of two topological surfaces is a frequent question that may be solved by using accurate topological invariants. Such invariants already exist and the main difficulty is to achieve their computation efficiently. In [VegYap90], authors propose an algorithm which allows to compute the canonical polygonal schema of a given surface by using particular transformation rules. This paper shows that these transformations can be defined on a 2-dimensional generalized map which encodes a surface. The algorithm proposed in [VegYap90] to compute canonical polygonal schema can now be transfered onto generalized maps. Moreover, all transformations can be achieved in O(1) with generalized maps, which can help optimizing existing algorithms. |    | 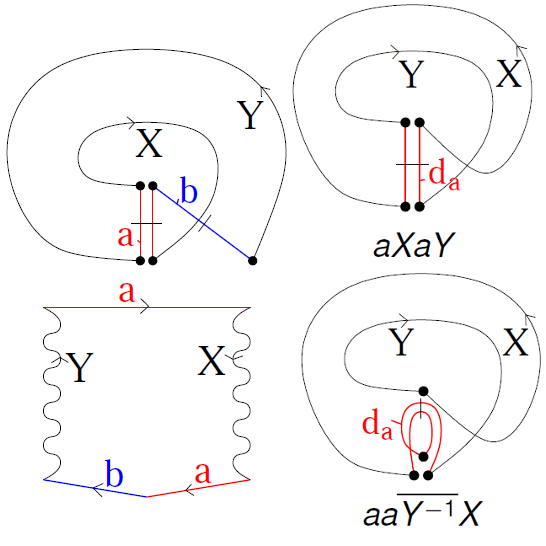 |
| [C22] Topologically Constrained Segmentation with Topological Maps Dupas A., Damiand G. Proc. of 1st International Workshop on Computational Topology in Image Context (CTIC), June 2008, Poitiers, France Abstract: This paper presents incremental algorithms used to compute Betti numbers with topological maps. Their implementation, as topological criterion for an existing bottom-up segmentation, is explained and results on artificial images are shown to illustrate the process. |   |  |
| [C21] First Results for 3D Image Segmentation with Topological Map Dupas A., Damiand G. Proc. of 14th International Conference on Discrete Geometry for Computer Imagery (DGCI), Lecture Notes in Computer Science 4992, pages 507-518, April 2008, Lyon, France Abstract: This paper presents the first segmentation operation defined within the 3D topological map framework. Firstly we show how a traditional segmentation algorithm, found in the literature, can be transposed on a 3D image represented by a topological map. We show the consistency of the results despite of the modifications made to the segmentation algorithm in order to handle topological maps. We study the complexity of the operation. Lastly, we present some experimental results mainly for 3D medical images. These results show the process duration of our method and validate the interest to use 3D topological map in the context of image processing. |    | 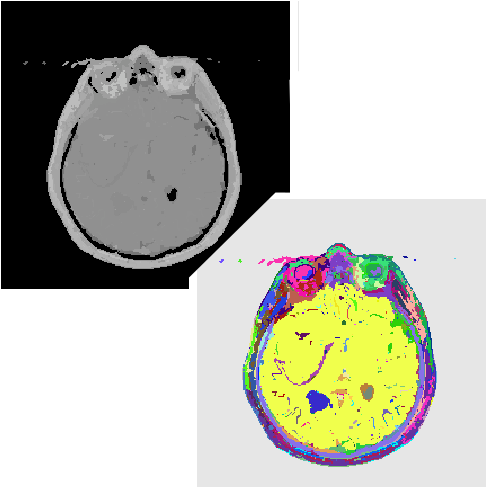 |
| [C20] Insertion and Expansion Operations for n -Dimensional Generalized Maps Baba-Ali M., Damiand G., Skapin X., Marcheix D. Proc. of 14th International Conference on Discrete Geometry for Computer Imagery (DGCI), Lecture Notes in Computer Science 4992, pages 141-152, April 2008, Lyon, France Abstract: Hierarchical representations, as irregular pyramids, are the bases of several applications in the field of discrete imagery. So, n-dimensional "bottom-up" irregular pyramids can be defined as stacks of successively reduced n-dimensional generalized maps (n-G-maps) [13], each n-G-map being defined from the previous level by using removal and contraction operations defined in [18]. Our goal is to build a theoretical framework for the definition and handling of n-dimensional "top-down" irregular pyramids. To do that, we propose in this paper to study the definition of insertion and expansion operations that allows to conceive this kind of pyramids. |    |  |
| [C19] Computing Homology Generators for Volumes using Minimal Generalized Maps Damiand G., Peltier S., Fuchs L. Proc. of 12th International Workshop on Combinatorial Image Analysis (IWCIA), Lecture Notes in Computer Science 4958, pages 63-74, April 2008, Buffalo, NY, USA Abstract: In this paper, we present an algorithm for computing efficiently homology generators of 3D subdivided orientable objects which can contain tunnels and cavities. Starting with an initial subdivision, represented with a generalized map where every cell is a topological ball, the number of cells is reduced using simplification operations (removal of cells), while preserving homology. We obtain a minimal representation which is homologous to the initial object. A set of homology generators is then directly deduced on the simplified 3D object. |    |  |
| [C18] Comparison of Local and Global Region Merging in the Topological Map Dupas A., Damiand G. Proc. of 12th International Workshop on Combinatorial Image Analysis (IWCIA), Lecture Notes in Computer Science 4958, pages 420-431, April 2008, Buffalo, NY, USA Abstract: Topological maps are a model which represents 2D or 3D image subdivisions. The aim of this structure is to provide an image representation which allows topological and geometrical features to be used by image processing operations. Algorithm of region merging is an useful tool in image segmentation and image processing. This paper presents two algorithms of region merging in 3D topological maps: one local which modifies locally the map around merged regions, and another one global which runs through all the elements of the map. We study their complexities and present experimental results to compare both approaches. |    |  |
| [C17] A New Contour Filling Algorithm Based on 2D Topological Map Damiand G., Arrivault D. Proc. of 6th Workshop on Graph-Based Representations in Pattern Recognition (GBR), Lecture Notes in Computer Science 4538, pages 319-329, June 2007, Alicante, Spain Abstract: In this paper, we present a topological algorithm which allows to fill contours images. The filling problem has been widely treated and it recently appeared that it can always be split into two different process : a generic topological process and a dedicated geometrical post-processing which depends on the application. Our algorithm, based on a 2D topological map description of the image, addresses the first step of processing. It is fast, generic and robust. Moreover, the complete topological description allows to easily integrate geometrical constrains and makes our approach an interesting basis for every filling process. |    | 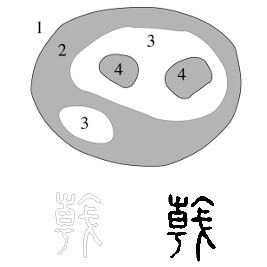 |
| [C16] Computing Homology Group Generators of Images Using Irregular Graph Pyramids Peltier S., Ion A., Haxhimusa Y., Kropatsch W.g., Damiand G. Proc. of 6th Workshop on Graph-Based Representations in Pattern Recognition (GBR), Lecture Notes in Computer Science 4538, pages 283-294, June 2007, Alicante, Spain Abstract: We introduce a method for computing homology groups and their generators of a 2D image, using a hierarchical structure i.e. irregular graph pyramid. Starting from an image, a hierarchy of the image is built, by two operations that preserve homology of each region. Instead of computing homology generators in the base where the number of entities (cells) is large, we first reduce the number of cells by a graph pyramid. Then homology generators are computed efficiently on the top level of the pyramid, since the number of cells is small, and a top down process is then used to deduce homology generators in any level of the pyramid, including the base level i.e. the initial image. We show that the new method produces valid homology generators and present some experimental results. |    | 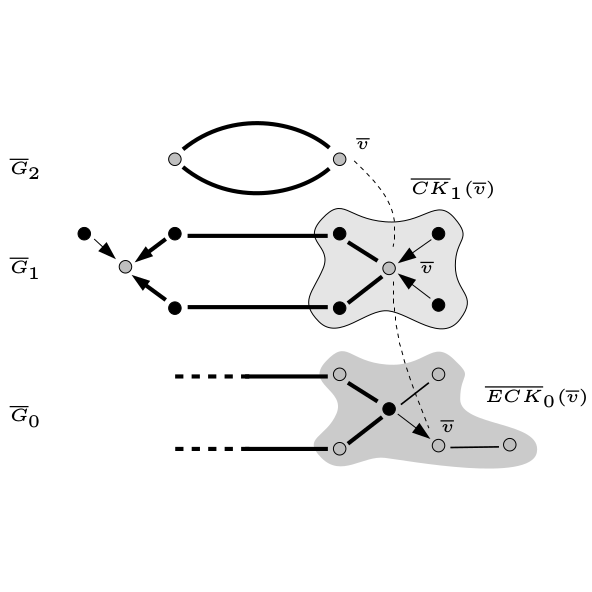 |
| [C15] Building 3D Indoor Scenes Topology from 2D Architectural Plans Horna S., Damiand G., Meneveaux D., Bertrand Y. Proc. of 2nd International Conference on Computer Graphics Theory and Applications (GRAPP), pages 37-44, March 2007, Barcelona, Spain Abstract: This paper presents a new method for reconstructing geometry and topology of 3D buildings from 2D architectural plans. A complete topological model expresses incidence and adjacency relations between all the elements. It is necessary for both recovering accurately 2D information and constructing a coherent 3D building. Based on an existing topological kernel, several high-level operations have been developped in 2D for creating walls, portals, stairs, etc. Semantic information is associated with all volumes for specifying openings, walls, rooms, stairs, facade, etc. The resulting 2D model is extruded for generating a 3D environment, taking the semantic information into account since doors are not processed as walls for instance. Floors are superimposed using volumes corresponding to upper and lower ceilings linked according to stairways. The resulting models are suitable for various application such as walkthrough, lighting/wave propoagation/thermal simulation. |   | 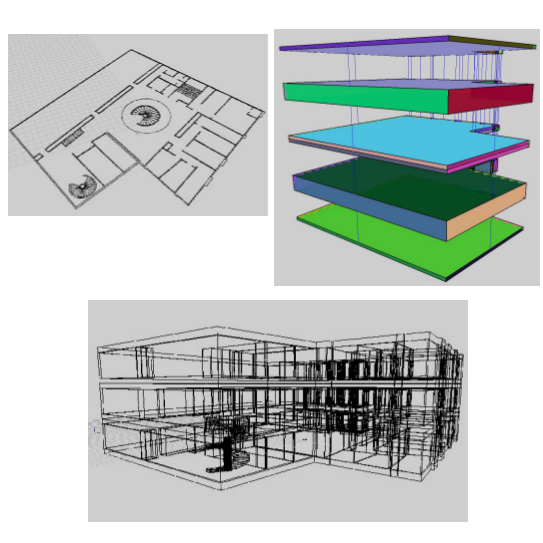 |
| [C14] Computing Homology for Surfaces with Generalized Maps: Application to 3D Images Damiand G., Peltier S., Fuchs L. Proc. of 2nd International Symposium on Visual Computing (ISVC), Lecture Notes in Computer Science 4292, pages 235-244, November 2006, Lake Tahoe, Nevada, USA Abstract: In this paper, we present an algorithm which allows to compute efficiently generators of the first homology group of a closed surface, orientable or not. Starting with an initial subdivision of a surface, we simplify it to its minimal form (minimal refers to the number of cells), while preserving its homology. Homology generators can thus be directly deduced from the minimal representation of the initial surface. Finally, we show how this algorithm can be used in a 3D labelled image in order to compute homology of each region described by its boundary. |    | 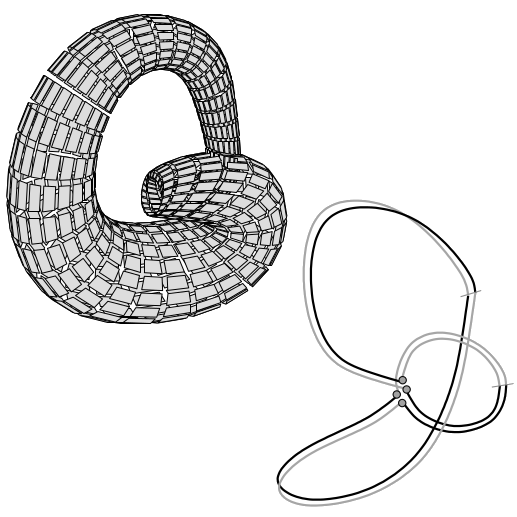 |
| [C13] Generalized Map Pyramid for Multi-level 3D Image Segmentation Simon C., Damiand G. Proc. of 13th International Conference on Discrete Geometry for Computer Imagery (DGCI), Lecture Notes in Computer Science 4245, pages 530-541, October 2006, Szeged, Hungary Abstract: Graph pyramids are often used to represent an image with various levels of details. Generalized pyramids have been recently defined in order to deal with images in any dimension. In this work, we show how to use generalized pyramids to represent 3D multi-level segmented images. We show how to construct such a pyramid, by alternating segmentation and simplification steps. We present how cells to be removed are marked: by using an homogeneous criterion to mark faces and the cell degree to mark other cells. When the pyramid is constructed, the main problem consists in retrieving information on regions. In this work, we show how to retrieve two types of information. The first one is the low level cells that are merged into a unique high level cell. The second one is the inter-voxel cells that compose a given region. |    | 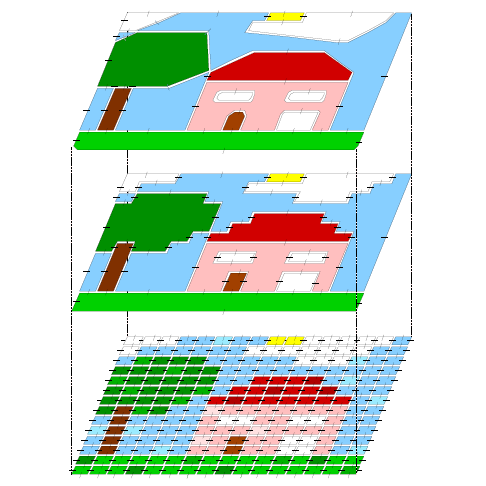 |
| [C12] Topological Map: An Efficient Tool to Compute Incrementally Topological Features on 3D Images Damiand G., Peltier P., Fuchs L., Lienhardt P. Proc. of 11th International Workshop on Combinatorial Image Analysis (IWCIA), Lecture Notes in Computer Science 4040, pages 1-15, June 2006, Berlin, Germany Abstract: In this paper, we show how to use the three dimensional topological map in order to compute efficiently topological features on objects contained in a 3D image. These features are useful for example in image processing to control operations or in computer vision to characterize objects. Topological map is a combinatorial model which represents both topological and geometrical information of a three dimensional labeled image. This model can be computed incrementally by using only two basic operations: the removal and the fictive edge shifting. In this work, we show that Euler characteristic can be computed incrementally during the topological map construction. This involves an efficient algorithm and open interesting perspectives for other features. |    |  |
| [C11] Receptive Fields for Generalized Map Pyramids: The Notion of Generalized Orbit Simon C., Damiand G., Lienhardt P. Proc. of 12th International Conference on Discrete Geometry for Computer Imagery (DGCI), Lecture Notes in Computer Science 3429, pages 56-67, April 2005, Poitiers, France Abstract: A pyramid of n-dimensional generalized maps is a hierarchical data structure. It can be used, for instance, in order to represent an irregular pyramid of n-dimensional images. A pyramid of generalized maps can be built by successively removing and/or contracting cells of any dimension. In this paper, we define generalized orbits, which extend the classical notion of receptive fields. Generalized orbits allow to establish the correspondence between a cell of a pyramid level and the set of cells of previous levels, the removal or contraction of which have led to the creation of this cell. In order to define generalized orbits, we extend, for generalized map pyramids, the notion of connecting walk defined by Brun and Kropatsch. |    |  |
| [C10] Pyramids of n-Dimensional Generalized Maps Simon C., Damiand G., Lienhardt P. Proc. of 5th Workshop on Graph-Based Representations in Pattern Recognition (GBR), Lecture Notes in Computer Science 3434, pages 142-152, April 2005, Poitiers, France Abstract: Graph pyramids are often used for representing irregular pyramids. Combinatorial pyramids have been recently defined for this purpose. We define here pyramids of n-dimensional generalized maps. This is the main contribution of this work: a generic definition in any dimension which extend and generalize the previous works. Moreover, such pyramids explicitly represent more topological information than graph pyramids. A pyramid can be implemented in several ways, and three representations are discussed in this paper. |    |  |
| [C9] Comparison and Convergence of Two Topological Models for 3D Image Segmentation Braquelaire A., Damiand G., Domenger J.-P., Vidil F. Proc. of 4th Workshop on Graph-Based Representations in Pattern Recognition (GBR), Lecture Notes in Computer Science 2726, pages 59-70, July 2003, York, England Abstract: In this paper we compare two topological models of 3D segmented images representation. These models are based on a collaboration between a topological representation and a geometrical representation of the regions of the segmented image. In both models the description of the topology lays on topological maps with a combinatorial representation. A geometrical embedding of maps is used to describe the geometry of regions. Both models differ in the way of defining this embedding. The aim of this paper is to compare these two models from the point of view of their interest for image segmentation, and to explore the possibility and the interest of making both these models converge |    | 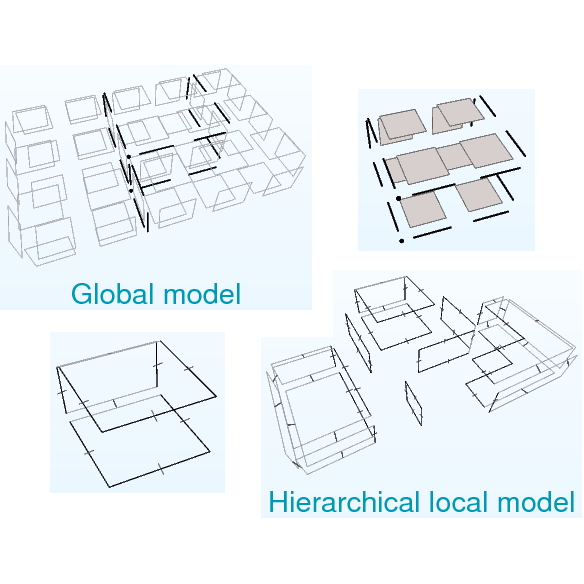 |
| [C8] Removal and Contraction for N-Dimensional Generalized Maps Damiand G., Lienhardt P. Proc. of 11th International Conference on Discrete Geometry for Computer Imagery (DGCI), Lecture Notes in Computer Science 2886, pages 408-419, November 2003, Naples, Italy Abstract: Removal and contraction are basic operations for several methods conceived in order to handle irregular image pyramids, for multi-level image analysis for instance. Such methods are often based upon graph-like representations which do not maintain all topological information, even for 2-dimensional images. We study the definitions of removal and contraction operations in the generalized maps framework. These combinatorial structures enable us to unambiguously represent the topology of a well-known class of subdivisions of n-dimensional (discrete) spaces. The results of this study make a basis for a further work about irregular pyramids of n-dimensional images. |    | 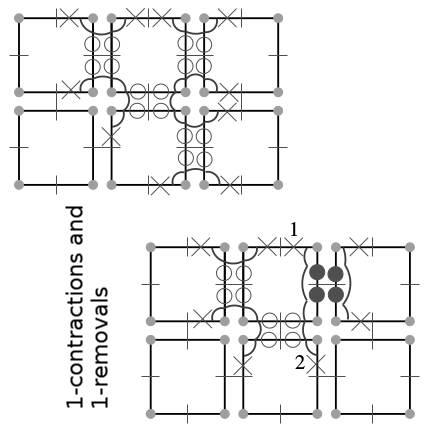 |
| [C7] Using 2D Topological Map Information in a Markovian Image Segmentation Damiand G., Alata O., Bihoreau C. Proc. of 11th International Conference on Discrete Geometry for Computer Imagery (DGCI), Lecture Notes in Computer Science 2886, pages 288-297, November 2003, Naples, Italy Abstract: Topological map is a mathematical model of labeled image representation which contains both topological and geometrical information. In this work, we use this model to improve a Markovian segmentation algorithm. Image segmentation methods based on Markovian assumption consist in optimizing a Gibbs energy function. This energy function can be given by a sum of potentials which could be based on the shape or the size of a region, the number of adjacencies,... and can be computed by using topological map. In this work we propose the integration of a new potential: the global linearity of the boundaries, and show how this potential can be extracted from the topological map. Moreover, to decrease the complexity of our algorithm, we propose a local modification of the topological map in order to avoid the reconstruction of the entire structure. |    | 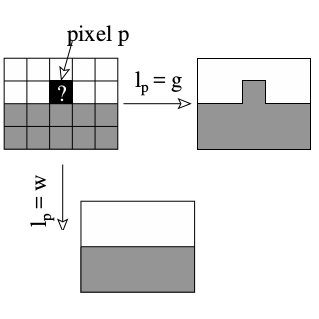 |
| [C6] Geometrical and Topological Informations for Image Segmentation with Monte Carlo Markov Chain Implementation Bourdon P., Alata O., Damiand G., Olivier C., Bertrand Y. Proc. of 15th International Conference on Vision Interface (VI), pages 413-420, May 2002, Calgary, Alberta, Canada Abstract: Image segmentation methods based on Markovian assumption consist in optimizing a Gibbs energy function which depends on the observation field and the segmented field. This energy function can be represented as a sum of potentials defined on cliques which are subsets of the grid of sites. The Potts model is the most commonly used to represent the segmented field. However, this model only expresses a potential on classes for nearest neighbor pixels. In this paper, we propose the integration of global informations, like the size of a region, in the local potentials of the Gibbs energy. To extract these informations, we use a representation model well known in geometric modeling: the topological map. Results on synthetic and natural images are provided, showing improvements in the obtained segmented fields. |    |  |
| [C5] Topological Map Based Algorithms for 3D Image Segmentation Damiand G., Resch P. Proc. of 10th International Conference on Discrete Geometry for Computer Imagery (DGCI), Lecture Notes in Computer Science 2301, pages 220-231, April 2002, Bordeaux, France Abstract: One of the most commonly used approach to segment a 2D image is the split and merge approach. In this paper, we are defining these two operations in 3D within the topological maps framework. This mathematic model of regions segmented image representation allows us to define these algorithms in a local and generic way. Moreover, we are defining a new operation, the corefining, which allows to treat big images. They are cut into small units, treated separately, then the result of each of them are combined to reconstruct the final representation. These three operations let us view efficient 3D segmentation algorithms, which is a difficult problem due to the size of data to treat. |    | 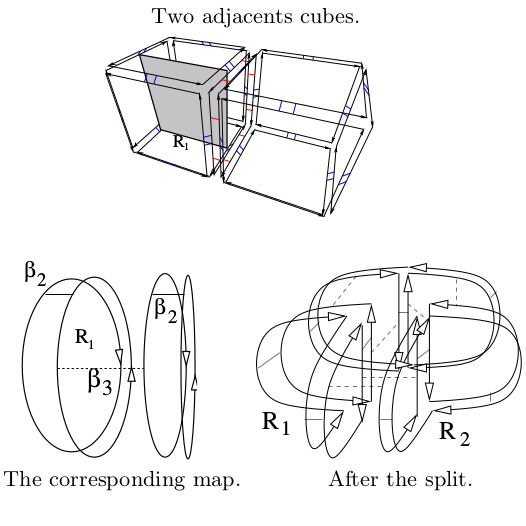 |
| [C4] Topological Map: Minimal Encoding of 3d Segmented Images Bertrand Y., Damiand G., Fiorio C. Proc. of 3rd Workshop on Graph-Based Representation in Pattern Recognition (GBR), pages 64-73, May 2001, Ischia, Italy Abstract: In this paper we define formally and completely the 3d topological map introduced in BertrandAl00: a model which encodes totally and minimally all the topological information of a 3d image. In particular, we focus on the problem of disconnections induced by the constructive definition based on several levels of maps. This multilevel representation is more or less a graph pyramid in sense that each level can be compute from the previous one in term of merge operations. Furthermore, algorithms extracting these maps from a segmented image have been given in BertrandAl00 and have been implemented and tested in practical applications. |   | 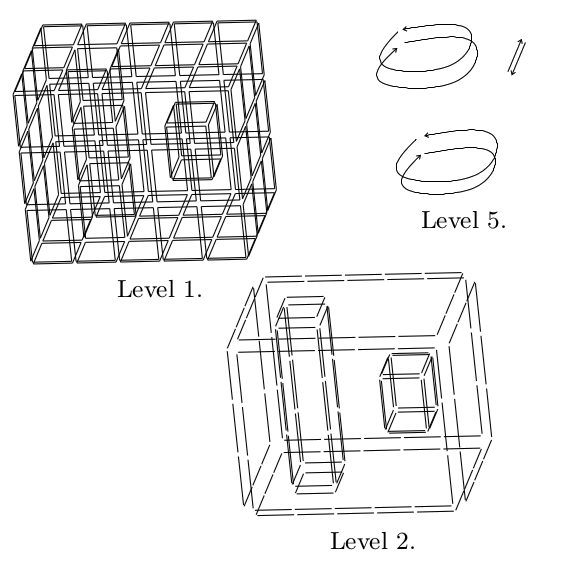 |
| [C3] Topological Encoding of 3d Segmented Images Bertrand Y., Damiand G., Fiorio C. Proc. of 9th International Conference on Discrete Geometry for Computer Imagery (DGCI), Lecture Notes in Computer Science 1953, pages 311-324, December 2000, Uppsala, Sweden Abstract: In this paper we define the 3d topological map and give an optimal algorithm which computes it from a segmented image. This data structure encodes totally all the information given by the segmentation. More, it allows to continue segmentation either algorithmically or interactively. We propose an original approach which uses several levels of maps. This allows us to propose a reasonable and implementable solution where other approaches don't allow suitable solutions. Moreover our solution has been implemented and the theoretical results translate very well in practical applications. |    | 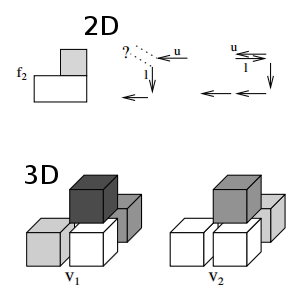 |
| [C2] Latest Developments and Results in Automatic SCF Counting. Part II: Improved Image Acquisition and Results Obtained Gourlot J.P, Héquet E., Giner M., Ahronovitz E., Hugon M., Damiand G. Proc. of Beltwide Cotton Conferences (BCC), pages 1522-1524, January 1998, San Diego, CA, USA Abstract: The Trashcam project developed a rapid, automated method used to evaluate the seed coat fragment (SCF) potential of fibers from new cotton plant lines. A camera is used to acquire an image of the fiber web and this is then analyzed by image processing. The latest version of the product, has improved image quality by using a scanner for image acquisition. We compare the automated counts obtained with counts made by an 'expert' in 166 cotton web images. Thanks to the new image acquisition technique and an algorithm whose parameters may be adjusted, the results obtained show that the square root of the automated counts are proportional to the square root of the visual counts. The relationship between the two counts obtained in the context of varietal improvement Bars was: square root of automated count = 1.00 square root of the visual count (r=0.965). |  |  |
| [C1] Latest Developments and Results in Automatic SCF Counting Giner M., Gourlot J.P., Bachelier B., Ahronovitz E., Hugon M., Damiand G. Proc. of Beltwide Cotton Conferences (BCC), pages 1633-1637, January 1997, New-Orleans, Louisiana, USA Abstract: Different image-processing methods were used to count seed coat fragments (SCF) in cotton fiber webs. The results obtained showed that, similar to SCF detection on yarn, it is possible to use this technique to prdict the 'SCF potential' of lines during varietal improvement programs. The last method was tested on 440 images derived from carded cottons of various geographic origins. Counts obtained automatically by the analysis of images acquired by a camera were similar to SCF counts made visually by an 'expert'; the relationship between the two counts being: square root of the automated count = 0.867* square root of the visual count + 0.393 (r=0.957). |  |  |
| Book Chapters |
| [BC2] Combinatorial Maps for 2D and 3D Image Segmentation Damiand G., Dupas A. Digital Geometry Algorithms: Theoretical Foundations and Applications to Computational Imaging, Lecture Notes in Computational Vision and Biomechanics 2, pages 359-393, May 2012 Abstract: This chapter shows how combinatorial maps can be used for 2D or 3D image segmentation. We start by introducing combinatorial maps and we show how they can be used to describe image partitions. Then, we present a generic segmentation algorithm that uses and modifies the image partition represented by a combinatorial map. One advantage of this algorithm is that one can mix different criteria and use different image features which can be associated with the cells of the partition. In particular, it is interesting that the topological properties of the image partition can be controlled through this approach. This property is illustrated by the computation of classical topological invariants, known as Betti numbers, which are then used to control the number of cavities or the number of tunnels of regions in the image partition. Finally, we present some experimental results of 2D and 3D image segmentation using different criteria detailed in this chapter. |    | 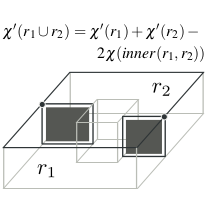 |
| [BC1] Cartes combinatoires pour l'analyse d'images Damiand G., Brun L. Géométrie discrète et images numériques, Traité IC2, Signal et Image, pages 103-120, Août 2007 Abstract: Les cartes combinatoires permettent de représenter totalement la topologie d'une subdivision cellulaire d'un objet graphique. Pour cette raison, elles s'avèrent être un bon outil pour représenter et modifier un découpage d'une image 2D ou 3D en régions. Dans ce chapitre nous montrons comment utiliser ces cartes combinatoires en analyse d'images. Nous montrons comment définir la carte, l'extraire à partir d'une image et quelles opérations il est possible d'utiliser pour modifier la partition. |    |  |
| Thesis |
| [T3] Contributions aux Cartes Combinatoires et Cartes Généralisées :
Simplification, Modèles, Invariants Topologiques et Applications Guillaume Damiand Habilitation à Diriger des Recherches, Lyon 1 University, 23 September 2010 Abstract: Ce mémoire résume nos principales contributions aux cartes combinatoires et cartes généralisées, deux modèles combinatoires représentant des subdivisions d'objets en cellules (sommets, arêtes, faces, volumes, ...). Ces modèles possèdent plusieurs avantages qui justifient leurs utilisations dans plusieurs domaines comme la modélisation géométrique et l'analyse d'images : ils sont définis en dimension quelconque à partir d'un seul type d'élément ; ils décrivent les cellules de la subdivision ainsi que toutes les relations d'adjacence et d'incidence entre ces cellules ; des contraintes de cohérence permettent de tester la validité des objets manipulés ; ils autorisent la mise en oeuvre d'algorithmes locaux, qui sont simples et efficaces en complexité. Nos travaux portent sur l'étude de ces modèles et sur la définition d'algorithmes. Nous avons tout d'abord défini quatre opérations de base : la suppression, la contraction, l'insertion et l'éclatement. Ces opérations sont les briques de base permettant de modifier un objet et peuvent être vues comme une généralisation des opérateurs d'Euler. Elles sont définies de manière générale en dimension quelconque. Il est ensuite possible d'ajouter des contraintes supplémentaires selon les applications et selon les propriétés spécifiques à conserver. Ces opérations sont au coeur de nos travaux. Nous les avons utilisées pour définir la carte topologique 2D et 3D, un modèle décrivant la partition d'une image en régions, puis pour définir des opérations de fusion et de découpe sur les cartes topologiques. Nous avons également défini les pyramides généralisées qui peuvent être vues comme des piles de cartes, chacune étant obtenue par simplification de la carte précédente. Enfin, nous avons proposé des algorithmes de calcul d'invariants topologiques : la caractéristique d'Euler-Poincaré, le schéma polygonal canonique, les nombres de Betti et les groupes d'homologies. Dans ces quatre cas, nous avons à nouveau utilisé les opérations de base afin de proposer des méthodes de mise à jour locales, ou pour simplifier la carte dans l'objectif d'accélérer les calculs du fait de la diminution du nombre de cellules. Nous avons utilisé ces travaux théoriques dans différentes applications. En modélisation géométrique, nous présentons le modeleur Moka qui est un modeleur géométrique à base topologique. Différentes applications se sont basées sur ce modeleur et nous présentons plus en détail une méthode de reconstruction automatique de bâtiments 3D à partir de plans numériques 2D. En traitement d'images, nous avons utilisé les cartes topologiques afin de proposer des algorithmes de segmentation d'images 2D et 3D pouvant intégrer un contrôle topologique. |    |  |
| [T2] Définition et étude d'un modèle topologique minimal de représentation d'images 2d et 3d Guillaume Damiand PhD Thesis, Montpellier II University, 14 December 2001 Abstract: Dans cette thèse, nous définissons et étudions un modèle topologique de représentation d'images segmentées en 2 et 3 dimensions : la carte topologique. La définition d'un tel modèle est primordiale afin de définir des algorithmes de segmentation efficaces. Ce problème a été beaucoup étudié en dimension 2, mais les solutions proposées sont difficilement extensibles en dimension 3.
Pour répondre à ce problème, nous définissons d'abord la carte topologique en dimension 2 en ayant comme préoccupation principale son extension en dimension supérieure. Nous introduisons une notion de niveau de simplification qui permet une définition progressive, chaque niveau s'obtenant simplement à partir du niveau précédent par application d'un type particulier de fusion. Cette notion permet de simplifier la définition de la carte topologique qui correspond au dernier niveau. Ces niveaux de simplification s'étendent sans difficulté majeure en dimension 3, et en dimension n. Ils facilitent également l'étude de la carte topologique et la preuve de ses propriétés. Ce modèle est en effet minimal, complet, invariant par rotation, translation et homothétie, et unique.
Nous présentons des algorithmes d'extraction permettant de construire ce modèle à partir d'images segmentées. Un premier algorithme << naïf >> effectue plusieurs passes sur l'image et n'est pas linéaire en dimension 3. Nous étudions ensuite un algorithme optimal d'extraction, basé sur la notion de précode, effectuant un seul balayage de l'image et un nombre minimal d'opérations. Les niveaux de simplification permettent de regrouper les nombreux cas à traiter, en étudiant pour chaque niveau les cas supplémentaires par rapport au niveau précédent. |    |  |
| [T1] Quelques propriétés des graphes distances héréditaires Guillaume Damiand Master Thesis, Montpellier II University, June 1997, Sibil: 1144509 |  |  |
| Editors |
| [E3] Image and Vision Computing: Special Issue: Discrete Geometry For Computer Imagery (IVC) Damiand G., Andres E. Image and Vision Computing, Volume 25, Number 10, October 2007 |  |  |
| [E2] Computers & Graphics: Special Issue: Discrete Geometry For Computer Imagery (C&G) Andres E., Damiand G., Lienhardt P. Computers & Graphics, Volume 30, Number 1, February 2006 |  |  |
| [E1] Proc. of 12th International conference Discrete Geometry for Computer Imagery (DGCI) Andres E., Damiand G., Lienhardt P. LNCS, Volume 3429, April 2005, Poitiers, France |  |  |
| Softwares |
| [S6] 3D Query Replace Damiand G., Nivoliers V. in replicabilitystamp.org, May 2022 Abstract: Program for the paper Query-Replace Operations for Topologically Controlled 3D Mesh Editing. |  |  |
| [S5] Surface Mesh Topology Damiand G., Lazarus F. in CGAL User and Reference Manual, September 2020 Abstract: This package provides a toolbox for manipulating curves on a combinatorial surface from the topological point of view. Two main functionalities are proposed. One is the computation of shortest curves that cannot be continuously deformed to a point. This includes the computation of the so-called edge width and face width of the vertex-edge graph of a combinatorial surface. The other functionality is the homotopy test for deciding if two given curves on a combinatorial surface can be continuously deformed one into the other. |  |  |
| [S4] Generalized Maps Damiand G. in CGAL User and Reference Manual, September 2016 Abstract: This package implements Generalized Maps in d dimensions. A generalized map is a data structure enabling to represent an orientable or non orientable subdivided object by describing all the cells of the subdivision (for example in 3D vertices, edges, faces, volumes) and all the incidence and adjacency relationships between these cells. Information can be associated to cells thanks to attributes. The package provides basic creation, modification operations, and several iterators enabling to run through some specific part of the object. |  |  |
| [S3] Linear Cell Complexes Damiand G. in CGAL User and Reference Manual, March 2012 Abstract: This package implements linear cell complexes, objects in d-dimension with linear geometry. The combinatorial part of objects is described either by a combinatorial or a generalized map, representing all the cells of the object plus the incidence and adjacency relations between cells. Geometry is added to the combinatorial data-structure simply by associating a point to each vertex of the map. Taking a 2D combinatorial map, and using 3D points, gives a linear cell complex equivalent to a Polyhedron_3. |  |  |
| [S2] Combinatorial Maps Damiand G. in CGAL User and Reference Manual, September 2011 Abstract: This package implements Combinatorial Maps in d dimensions. A combinatorial map is a data structure enabling to represent an orientable subdivided object by describing all the cells of the subdivision (for example in 3D vertices, edges, faces, volumes) and all the incidence and adjacency relationships between these cells. Information can be associated to cells thanks to attributes. In 2D, a combinatorial map is equivalent to a halfedge data structure. The package provides basic creation, modification operations, and several iterators enabling to run through some specific part of the object. |  |  |
| [S1] Moka: 3D Topological Modeler Vidil F., Damiand G., Dexet-Guiard M., Guiard N., Ledoux F., Fousse A., Fradin D., Liang Y., Meneveaux D., Bertrand Y. December 2002 Abstract: MOKA is a 3D geometrical modeler on licence GPL and LGP, based on a topological kernel. It allows, like classical modelers, the creation and the modification of 3D objects thanks to many operations. The originality of our modeler is its kernel whith is defined with 3D generalized maps (called 3G-maps). This model, defined in any dimension, represents the space subdivisions with a unique basic element: the darts. |  |  |
 [Back]
[Back]